Question

在平面直角坐标系中，O为坐标原点，已知两点M（1,-3）、N（5，1），若点C满足=?t+(1-t)(t∈R),点C的轨迹与抛物线y²=4x交于A、B两点.

（1）求证：⊥;

（2）在x轴上是否存在一点P（m,0），使得过点P任作抛物线的一条弦，并以该弦为直径的圆都过原点.若存在，请求出m的值及圆心的轨迹方程；若不存在，请说明理由.

Answer 1

（1）证明：由=t+(1-t)(t∈R)知点C的轨迹是M、N两点所在的直线，故点C的轨迹方程是：y+3=·(x-1),即y=x-4.

由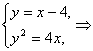(x-4)²=4xx²-12x+16=0.

∴x₁x₂=16，x₁+x₂=12，

∴y₁y₂=(x₁-4)(x₂-4)=x₁x₂-4(x₁+x₂)+16=-16.

∴x₁x₂+y₁y₂=0.故⊥.

（2）解析：存在点P（4，0），使得过点P任作抛物线的一条弦，以该弦为直径的圆都过原点.

由题意知：弦所在的直线的斜率不为零，

故设弦所在的直线方程为：x=ky+4，代入y²=x，得y²-4ky-16=0,

∴y₁+y₂=4k,y₁y₂=-16.

k_OA·k_OB=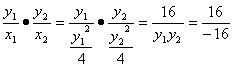=-1.

∴OA⊥OB,故以AB为直径的圆都过原点.

设弦AB的中点为M(x,y)，

则x=(x₁+x₂),y=(y₁+y₂).

x₁+x₂=ky₁+4+ky₂+4=k(y₁+y₂)+8=k·(4k）+8=4k²+8.

∴弦AB的中点M的轨迹方程为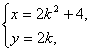：消去k，得y²=2x-8.