题目内容
14.在极坐标系下,过直线ρcosθ+ρsinθ=2$\sqrt{2}$上任意一点M,作曲线ρ=1的两条切线,则这两条切线的夹角的最大值为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{2π}{3}$ |
分析 利用$\left\{\begin{array}{l}{x=ρcosθ}\\{y=ρsinθ}\end{array}\right.$即可把直线l:ρcosθ+ρsinθ=2$\sqrt{2}$化为直角坐标方程,曲线ρ=1h化为直角坐标方程.要使∠AMB最大,即使AM最短,即OM最短.过O最OM⊥l,则垂足M满足要求.
解答 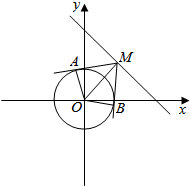 解:直线l:ρcosθ+ρsinθ=2$\sqrt{2}$化为直角坐标方程:x+y=2$\sqrt{2}$,曲线ρ=1h化为x2+y2=1,R=1.
解:直线l:ρcosθ+ρsinθ=2$\sqrt{2}$化为直角坐标方程:x+y=2$\sqrt{2}$,曲线ρ=1h化为x2+y2=1,R=1.
要使∠AMB最大,即使AM最短,即OM最短.
∴过O最OM⊥l,则垂足M满足要求.
由原点到l的距离d=$\frac{2\sqrt{2}}{\sqrt{2}}$=2=2R,
∴∠AMO=$\frac{π}{6}$,∠AMB=$\frac{π}{3}$.
∴这两条切线的夹角的最大值为$\frac{π}{3}$.
故选:B.
点评 本题考查了极坐标方程化为直角坐标方程、直线与圆相切的性质、勾股定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
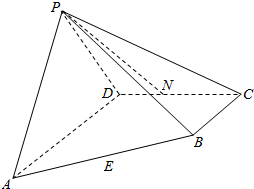 如图,四棱锥P-ABCD的侧面PAD垂直于底面ABCD,∠ADC=∠BCD=90°,PA=PD=AD=2BC=2,CD=$\sqrt{2}$,N为线段CD的中点.
如图,四棱锥P-ABCD的侧面PAD垂直于底面ABCD,∠ADC=∠BCD=90°,PA=PD=AD=2BC=2,CD=$\sqrt{2}$,N为线段CD的中点.