题目内容
已知函数f(x)=-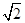 sin(2x+
sin(2x+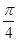 )+6sinxcosx-2cos2x+1,x∈R.
)+6sinxcosx-2cos2x+1,x∈R.
(1)求f(x)的最小正周期;
(2)求f(x)在区间[0,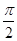 ]上的最大值和最小值.
]上的最大值和最小值.
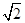 sin(2x+
sin(2x+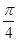 )+6sinxcosx-2cos2x+1,x∈R.
)+6sinxcosx-2cos2x+1,x∈R.(1)求f(x)的最小正周期;
(2)求f(x)在区间[0,
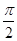 ]上的最大值和最小值.
]上的最大值和最小值.(1)π (2)最大值为2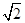 ,最小值为-2
,最小值为-2
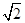 ,最小值为-2
,最小值为-2解:(1)f(x)=-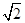 sin2x·cos
sin2x·cos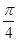 -
-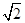 cos2x·sin
cos2x·sin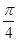 +3sin2x-cos2x
+3sin2x-cos2x
=2sin2x-2cos2x=2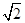 sin(2x-
sin(2x-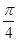 ).
).
∴f(x)的最小正周期T=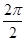 =π.
=π.
(2)∵0≤x≤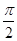 ,∴-
,∴-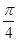 ≤2x-
≤2x-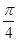 ≤
≤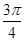 ,
,
∴-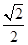 ≤sin(2x-
≤sin(2x-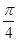 )≤1,
)≤1,
∴-2≤f(x)≤2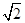 ,
,
故函数f(x)在区间[0,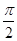 ]上的最大值为2
]上的最大值为2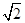 ,最小值为-2.
,最小值为-2.
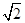 sin2x·cos
sin2x·cos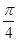 -
-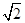 cos2x·sin
cos2x·sin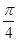 +3sin2x-cos2x
+3sin2x-cos2x=2sin2x-2cos2x=2
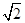 sin(2x-
sin(2x-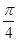 ).
).∴f(x)的最小正周期T=
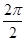 =π.
=π.(2)∵0≤x≤
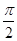 ,∴-
,∴-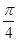 ≤2x-
≤2x-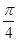 ≤
≤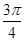 ,
,∴-
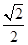 ≤sin(2x-
≤sin(2x-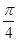 )≤1,
)≤1,∴-2≤f(x)≤2
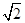 ,
,故函数f(x)在区间[0,
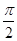 ]上的最大值为2
]上的最大值为2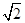 ,最小值为-2.
,最小值为-2.
练习册系列答案
相关题目
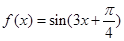 .
.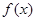 的单调递增区间;
的单调递增区间;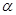 是第二象限角,
是第二象限角,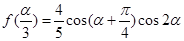 ,求
,求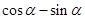 的值.
的值.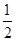 +cosα,且α∈(0,
+cosα,且α∈(0,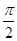 ),则
),则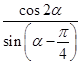 的值为________.
的值为________.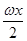 +
+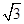 sinωx-3(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B、C为图象与x轴的交点,且△ABC为正三角形.
sinωx-3(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B、C为图象与x轴的交点,且△ABC为正三角形.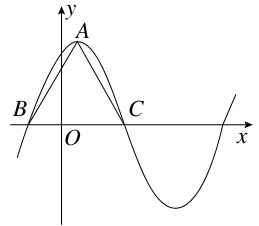
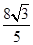 ,且x0∈(-
,且x0∈(-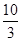 ,
,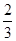 ),求f(x0+1)的值.
),求f(x0+1)的值.

 是方程
是方程 的两根,则
的两根,则 .
.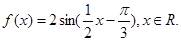
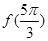 的值;
的值;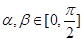 ,
,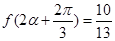 ,
,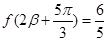 ,
,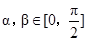 ,求
,求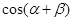 的值.
的值.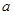 ,
,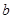 ,
,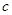 分别为
分别为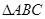 三个内角
三个内角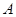 ,
,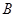 ,
,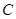 的对边,
的对边, 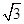
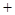
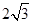 ,
,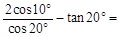 .
.