Question

函数y=|x²-1|与y=a的图象有4个交点，则实数a的取值范围是    ．

Answer 1

【答案】分析：若函数y=|x²-1|与函数y=a有4个交点，可由函数图象的对折变换先画出函数y=|x²-1|的图象，结合图象可得实数a的取值范围．
解答：解：函数y=|x²-1|的图象如下图所示：

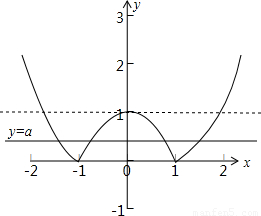
结合图象可得：
当0＜a＜1时函数y=|x²-1|与y=a的图象有4个交点，
故答案为 （0，1）．
点评：本题考查了根的存在性及根的个数判断，以及函数与方程的思想，解答关键是运用数形结合的思想，属于中档题．