题目内容
若lga+lgb=0(其中a≠1,b≠1),则函数f(x)=ax与g(x)=bx的图象( )
| A．关于直线y=x对称 | B．关于x轴对称 |
| C．关于y轴对称 | D．关于原点对称 |
C
解析
练习册系列答案
相关题目
设
则a，b，c的大小关系为
| A．a＜c＜b | B．b＜a＜c | C．a＜b＜c | D．b＜c＜a |
如图，偶函数f(x)的图像形如字母M,奇函数g（x）的图像形如字母N，若方程
的实根个数分别为a，b，c，d，则a＋b＋c＋d＝( )
| A．27 | B．30 | C．33 | D．36 |
函数
的定义域为
A． | B． | C． | D． |
函数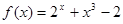
在区间
内的零点个数是（ ）
A． | B． | C． | D． |
某公司生产一种产品，固定成本为20 000元，每生产一单位的产品，成本增加100元，若总收入R与年产量x的关系是R(x)＝
则当总利润最大时，每年生产产品的单位数是 ( )．
| A．150 | B．200 |
| C．250 | D．300 |
某学校制定奖励条例,对在教育教学中取得优异成绩的教职工实行奖励,其中有一个奖励项目是针对学生高考成绩的高低对任课教师进行奖励的.奖励公式为f(n)=k(n)(n-10),n>10(其中n是任课教师所在班级学生的该任课教师所教学科的平均成绩与该科省平均分之差,f(n)的单位为元),而k(n)=
现有甲、乙两位数学任课教师,甲所教的学生高考数学平均分超出省平均分18分,而乙所教的学生高考数学平均分超出省平均分21分,则乙所得奖励比甲所得奖励多( )
| A．600元 | B．900元 | C．1600元 | D．1700元 |
若x0是函数f(x)=(
)x-
的零点,则x0属于区间( )
| A．(-1,0) | B．(0,1) |
| C．(1,2) | D．(2,3) |
已知函数f(x)＝
若函数g(x)＝f(x)－m有三个不同的零点，则实数m的取值范围为( )
A．－ ，1 | B．－，1 | C．－ ，0 | D．－，0 |