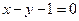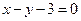题目内容
(本小题满分12分)
已知圆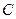 的方程为
的方程为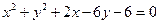 ,
,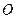 为坐标原点.
为坐标原点.
(Ⅰ)求过点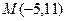 的圆
的圆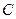 的切线方程;
的切线方程;
(Ⅱ)若圆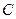 上有两点
上有两点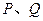 关于直线
关于直线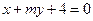 对称,并且满足
对称,并且满足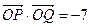 ,求
,求
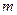 的值和直线
的值和直线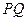 的方程;
的方程;
(Ⅲ)过点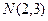 作直线与圆
作直线与圆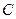 交于
交于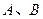 两点,求
两点,求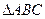 的最大面积以及此时直线
的最大面积以及此时直线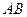 的斜率.
的斜率.
已知圆
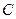 的方程为
的方程为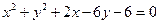 ,
,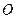 为坐标原点.
为坐标原点.(Ⅰ)求过点
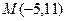 的圆
的圆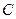 的切线方程;
的切线方程;(Ⅱ)若圆
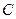 上有两点
上有两点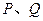 关于直线
关于直线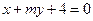 对称,并且满足
对称,并且满足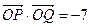 ,求
,求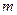 的值和直线
的值和直线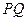 的方程;
的方程;(Ⅲ)过点
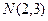 作直线与圆
作直线与圆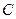 交于
交于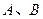 两点,求
两点,求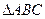 的最大面积以及此时直线
的最大面积以及此时直线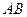 的斜率.
的斜率.(1)
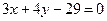
(2)
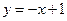
(3)
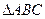 的最大面积为8,此时直线
的最大面积为8,此时直线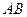 的斜率为
的斜率为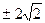 .
.解:(Ⅰ)圆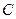 的标准方程为
的标准方程为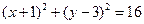 ,圆心为
,圆心为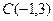 ,半径
,半径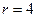
设过点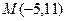 的切方程为
的切方程为 ,即
,即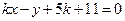 ,
,
则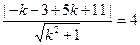 ,解得
,解得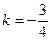
切线方程为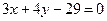 ----------------3分
----------------3分
当斜率不存在时,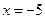 也符合题意.
也符合题意.
故求过点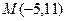 的圆
的圆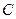 的切线方程为:
的切线方程为: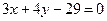 或
或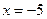 . ----------------4分
. ----------------4分
(Ⅱ)因为点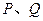 在圆上且关于直线
在圆上且关于直线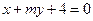 对称,
对称,
∴圆心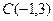 在直线上,代入得
在直线上,代入得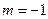 .------------------------------5分
.------------------------------5分
因为直线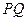 与直线
与直线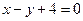 垂直,
垂直,
所以可以设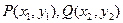 ,
,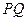 方程为
方程为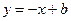 .
.
将直线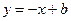 代入圆C的方程,得
代入圆C的方程,得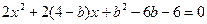 .------------------------------------------6分
.------------------------------------------6分
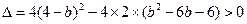 ,得
,得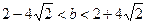 .
.
由根与系数的关系得

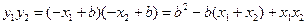
因为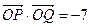
所以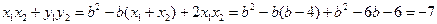
即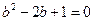 ,解得
,解得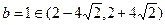 ,
,
故所求的直线方程为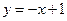 .--------------------------------8分
.--------------------------------8分
(Ⅲ)当直线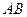 的斜率不存在时,
的斜率不存在时,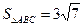 , ----------------------------9分
, ----------------------------9分
当直线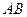 的斜率存在时,设直线
的斜率存在时,设直线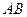 的方程为
的方程为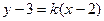 ,即
,即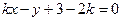 ,
,
圆心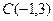 到直线
到直线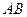 的距离
的距离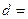
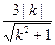 ,线段
,线段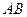 的长度
的长度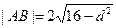 ,
,
所以,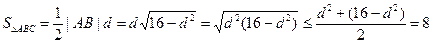 ,
,
当且仅当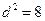 时取等号,此时
时取等号,此时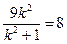 ,解得
,解得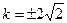
所以,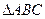 的最大面积为8,此时直线
的最大面积为8,此时直线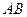 的斜率为
的斜率为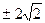 . --------12分
. --------12分
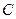 的标准方程为
的标准方程为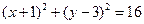 ,圆心为
,圆心为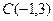 ,半径
,半径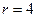
设过点
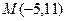 的切方程为
的切方程为 ,即
,即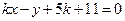 ,
,则
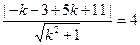 ,解得
,解得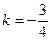
切线方程为
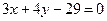 ----------------3分
----------------3分当斜率不存在时,
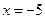 也符合题意.
也符合题意.故求过点
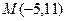 的圆
的圆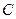 的切线方程为:
的切线方程为: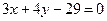 或
或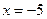 . ----------------4分
. ----------------4分(Ⅱ)因为点
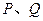 在圆上且关于直线
在圆上且关于直线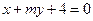 对称,
对称,∴圆心
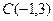 在直线上,代入得
在直线上,代入得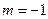 .------------------------------5分
.------------------------------5分因为直线
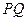 与直线
与直线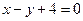 垂直,
垂直,所以可以设
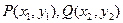 ,
,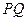 方程为
方程为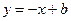 .
.将直线
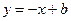 代入圆C的方程,得
代入圆C的方程,得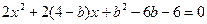 .------------------------------------------6分
.------------------------------------------6分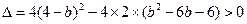 ,得
,得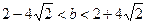 .
.由根与系数的关系得

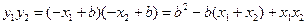
因为
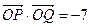
所以
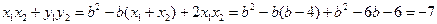
即
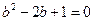 ,解得
,解得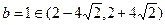 ,
,故所求的直线方程为
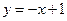 .--------------------------------8分
.--------------------------------8分(Ⅲ)当直线
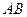 的斜率不存在时,
的斜率不存在时,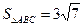 , ----------------------------9分
, ----------------------------9分当直线
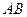 的斜率存在时,设直线
的斜率存在时,设直线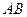 的方程为
的方程为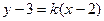 ,即
,即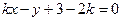 ,
,圆心
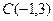 到直线
到直线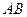 的距离
的距离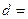
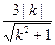 ,线段
,线段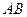 的长度
的长度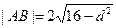 ,
,所以,
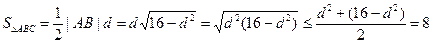 ,
,当且仅当
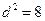 时取等号,此时
时取等号,此时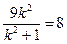 ,解得
,解得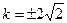
所以,
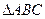 的最大面积为8,此时直线
的最大面积为8,此时直线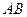 的斜率为
的斜率为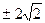 . --------12分
. --------12分
练习册系列答案
相关题目
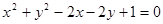 上的动点Q到直线
上的动点Q到直线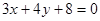 距离的最小值为
距离的最小值为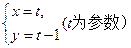 与x轴的交点,且圆C与直线
与x轴的交点,且圆C与直线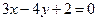 相切,则圆C的方程为 .
相切,则圆C的方程为 .
 与圆
与圆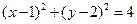 相交于
相交于 、
、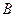 两点,且弦
两点,且弦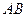 的长为
的长为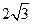 ,则
,则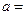
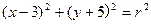 上有且仅有两个点到直线4x-3y-2=0的距离为1,则半径r的取值范围是( )
上有且仅有两个点到直线4x-3y-2=0的距离为1,则半径r的取值范围是( ) 和圆
和圆 相交于点
相交于点 ,则弦
,则弦 的垂直平分线方程是
的垂直平分线方程是 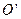 都经
都经 过A、B两点,AC是⊙
过A、B两点,AC是⊙
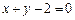 和圆
和圆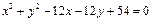 都相切且半径最
都相切且半径最 小的圆的方程是______________.
小的圆的方程是______________.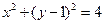 中过点Q(1,2),且与圆相交截得的弦长最短时的直线方程是( )
中过点Q(1,2),且与圆相交截得的弦长最短时的直线方程是( )