题目内容
已知A(-2,0),B(0,2); C是圆上x2+y2-2x=0上任意一点,则△ABC的面积的最大值是
- A.3+

- B.3-

- C.6
- D.4
A
分析:当C到AB距离最大时,△ABC的面积取到最大值,由于点C是圆上的动点,根据图形可知C到AB距离最大,为圆心到直线的距离加上半径,故可求.
解答:由题意,当C到AB距离最大时,△ABC的面积取到最大值
由 x2+y2-2x=0可得(x-1)2+y2=1,知圆心为M (1,0),半径为1,直线AB的方程为x-y+2=0
圆心M到直线AB的距离为d=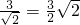
故C点到AB的距离最大为
又AB距离为 ,所以三角形ABC的最大值为
,所以三角形ABC的最大值为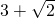
故选A.
点评:本题的考点是圆方程的综合应用,主要考查圆的标准方程,考查三角形的面积,关键是利用当C到AB距离最大时,△ABC的面积取到最大值
分析:当C到AB距离最大时,△ABC的面积取到最大值,由于点C是圆上的动点,根据图形可知C到AB距离最大,为圆心到直线的距离加上半径,故可求.
解答:由题意,当C到AB距离最大时,△ABC的面积取到最大值
由 x2+y2-2x=0可得(x-1)2+y2=1,知圆心为M (1,0),半径为1,直线AB的方程为x-y+2=0
圆心M到直线AB的距离为d=
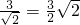
故C点到AB的距离最大为

又AB距离为
 ,所以三角形ABC的最大值为
,所以三角形ABC的最大值为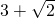
故选A.
点评:本题的考点是圆方程的综合应用,主要考查圆的标准方程,考查三角形的面积,关键是利用当C到AB距离最大时,△ABC的面积取到最大值

练习册系列答案
相关题目