题目内容
在直角坐标系中,以M(-1,0)为圆心的圆与直线x-| 3 |
(1)求圆M的方程;
(2)已知A(-2,0)、B(2,0),圆内动点P满足|PA|•|PB|=|PO|2,求
| PA |
| PB |
分析:(1)根据直线与圆线切,可转化成圆心到直线的距离等于半径,建立等量关系,求出半径即可;
(2)设出点P的坐标,由|PA|•|PB|=|PO|2求出点P的轨迹,根据数量积的运算公式表示出
•
,再利用消元法得到一个变量的函数求取值范围,注意这一变量的范围.
(2)设出点P的坐标,由|PA|•|PB|=|PO|2求出点P的轨迹,根据数量积的运算公式表示出
| PA |
| PB |
解答:解:(1)依题意,圆M的半径等于圆心M(-1,0)到直线x-
y-3=0的距离,
即r=
=2.(4分)
∴圆M的方程为(x+1)2+y2=4.(6分)
(2)设P(x,y),由|PA|•|PB|=|PO|2,
得
•
=x2+y2,
即x2-y2=2.(9分)
•
=(-2-x,-y)•(2-x,-y)=y2+x2-4=2(y2-1)(11分)
∵点在圆M内,
∴(x+1)2+y2<4,而x2-y2=2
∴
<x<
,
?0≤y2<1+
?-1≤y2-1<
,
∴
•
的取值范围为[-2,
).(14分)
| 3 |
即r=
| |-1-3| | ||
|
∴圆M的方程为(x+1)2+y2=4.(6分)
(2)设P(x,y),由|PA|•|PB|=|PO|2,
得
| (x+2)2+y2 |
| (x-2)2+y2 |
即x2-y2=2.(9分)
| PA |
| PB |
∵点在圆M内,
∴(x+1)2+y2<4,而x2-y2=2
∴
-1-
| ||
| 2 |
-1+
| ||
| 2 |
?0≤y2<1+
| ||
| 2 |
| ||
| 2 |
∴
| PA |
| PB |
| 11 |
点评:本题主要考查了圆的标准方程以及直线与圆的位置关系,平面向量数量积的运算等知识,属于中档题.

练习册系列答案
相关题目
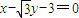 相切.
相切.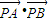 的取值范围.
的取值范围.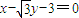 相切.
相切.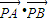 的取值范围.
的取值范围.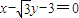 相切.
相切.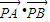 的取值范围.
的取值范围.