题目内容
如图是一个从A→B的”闯关”游戏.规则规定:每过一关前都要抛掷一个在各面上分别标有1,2,3,4的均匀的正四面体.在过第n(n=1,2,3)关时,需要抛掷n次正四面体,如果这n次面朝下的数字之和大于2n,则闯关成功.
(1)求闯第一关成功的概率;
(2)记闯关成功的关数为随机变量X,求X的分布列和期望.

(1)求闯第一关成功的概率;
(2)记闯关成功的关数为随机变量X,求X的分布列和期望.

(1)抛一次正四面体面朝下的数字有1,2,3,4四种情况,
大于2的有两种情况,
∴闯第一关成功的概率p=
.
(2)记事件“抛掷n次正四面体,这n次面朝下的数学之和大于2n”为事件An,
则P(A1)=
;
抛掷两次正四面体面朝下的数字之和的情况如图所示:
∴P(A2)=
=
,
设抛掷三次正四面体面朝下的数字依次记为:x,y,z,
考虑x+y+z>8的情况,
当x=1时,y+z>7有1种情况,
当x=2时,y+z>6有3种情况,
当x=3时,y+z>5有6种情况,
当x=4时,y+z>4有10种情况,
∴P(A3)=
=
,
由题意知X的所有可能取值为0,1,2,3,
P(X=0)=P(
)=
,
P(X=1)=P(A1
)=
×
=
,
P(X=2)=P(A1A2
)=
×
×
=
,
P(X=3)=P(A1A2A3)=
×
×
=
,
∴X的分布列为:
EX=0×
+1×
+2×
+3×
=
.
大于2的有两种情况,
∴闯第一关成功的概率p=
| 1 |
| 2 |
(2)记事件“抛掷n次正四面体,这n次面朝下的数学之和大于2n”为事件An,
则P(A1)=
| 1 |
| 2 |

抛掷两次正四面体面朝下的数字之和的情况如图所示:
∴P(A2)=
| 10 |
| 16 |
| 5 |
| 8 |
设抛掷三次正四面体面朝下的数字依次记为:x,y,z,
考虑x+y+z>8的情况,
当x=1时,y+z>7有1种情况,
当x=2时,y+z>6有3种情况,
当x=3时,y+z>5有6种情况,
当x=4时,y+z>4有10种情况,
∴P(A3)=
| 1+3+6+10 |
| 43 |
| 5 |
| 16 |
由题意知X的所有可能取值为0,1,2,3,
P(X=0)=P(
| . |
| A1 |
| 1 |
| 2 |
P(X=1)=P(A1
| . |
| A2 |
| 1 |
| 2 |
| 3 |
| 8 |
| 3 |
| 16 |
P(X=2)=P(A1A2
| . |
| A3 |
| 1 |
| 2 |
| 5 |
| 8 |
| 11 |
| 16 |
| 55 |
| 256 |
P(X=3)=P(A1A2A3)=
| 1 |
| 2 |
| 5 |
| 8 |
| 5 |
| 16 |
| 25 |
| 256 |
∴X的分布列为:
| X | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 1 |
| 2 |
| 3 |
| 16 |
| 55 |
| 256 |
| 25 |
| 256 |
| 233 |
| 256 |

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
 .(Ⅰ)求p的值;(Ⅱ)求
.(Ⅰ)求p的值;(Ⅱ)求
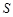 的值是( )
的值是( )


