题目内容
【题目】在四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上,且
上,且![]() ,
,![]() 为线段
为线段![]() 的中点.
的中点.

(1)求证:![]() 平面
平面![]() ;
;
(2)若![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
【答案】(1)见解析(2)![]()
【解析】
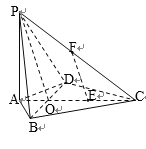
(1)设AC∩BD=O,连接PO,通过证明EF为△POC的中位线,推出EF∥PO,然后EF∥平面PBD.
(2)利用VF﹣PAD![]() VC﹣PAD
VC﹣PAD![]() VP﹣CAD,求解几何体的体积即可.
VP﹣CAD,求解几何体的体积即可.
(1) ∵AB=AD,CB=CD,∴AC⊥BD,设AC∩BD=O,连接PO,
由AB=AD=2,∠BAD=120
得:OA=1,BD=2![]() ,在RtCOD中,CD=
,在RtCOD中,CD=![]() , OD=
, OD=![]()
∴OC=2
∵AE=2EC,
∴E为OC中点
又∵F为PC的中点
∴EF为POC的中位线
∴EF∥PO
又PO面PBD EF面PBD
∴EF∥平面PBD
(2)在Rt△PAC中,PC=5,由(1)可知AC=3,∴PA=4
∴VF-PAD=![]() VC-PAD=
VC-PAD=![]() VP-CAD=
VP-CAD=![]() ×
×![]() VP-ABCD=
VP-ABCD=![]() ×
×![]() ×
×![]() ×3×2
×3×2![]() ×4=
×4=![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
