题目内容
下面是关于公差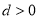 的等差数列
的等差数列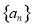 的四个命题:
的四个命题:
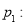 数列
数列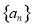 是递增数列;
是递增数列;
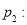 数列
数列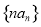 是递增数列;
是递增数列;
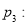 数列
数列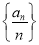 是递增数列;
是递增数列;
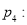 数列
数列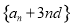 是递增数列;
是递增数列;
其中的真命题为( )
A.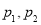 B.
B.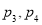
C.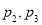 D.
D.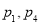
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
下面是关于公差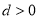 的等差数列
的等差数列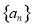 的四个命题:
的四个命题:
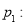 数列
数列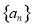 是递增数列;
是递增数列;
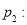 数列
数列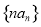 是递增数列;
是递增数列;
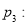 数列
数列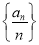 是递增数列;
是递增数列;
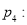 数列
数列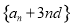 是递增数列;
是递增数列;
其中的真命题为( )
A.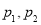 B.
B.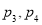
C.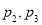 D.
D.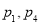
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案