题目内容
(本题满分15分)如图,已知直线![]() (
(![]() )与抛物线
)与抛物线![]() :
:![]() 和圆
和圆![]() :
:![]() 都相切,
都相切,![]() 是
是![]() 的焦点.
的焦点.
(Ⅰ)求![]() 与
与![]() 的值;
的值;
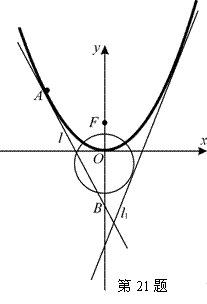 (Ⅱ)设
(Ⅱ)设![]() 是
是![]() 上的一动点,以
上的一动点,以![]() 为切点作抛物线
为切点作抛物线![]()
的切线![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,以
,以![]() 、
、![]() 为
为
邻边作平行四边形![]() ,证明:点
,证明:点![]() 在一条
在一条
定直线上;
(Ⅲ)在(Ⅱ)的条件下,记点![]() 所在的定直线为
所在的定直线为![]() ,
,
直线![]() 与
与![]() 轴交点为
轴交点为![]() ,连接
,连接![]() 交抛物线
交抛物线![]()
于![]() 、
、![]() 两点,求△
两点,求△![]() 的面积
的面积![]() 的取值范围.
的取值范围.
(本题满分15分)
解:(Ⅰ)由已知,圆![]() :
: ![]() 的圆心为
的圆心为![]() ,半径
,半径![]() .
.
由题设圆
心到直线![]() 的距离
的距离![]() .
.
即![]() ,解得
,解得![]() (
(![]() 舍去). …………………(2分)
舍去). …………………(2分)
设![]() 与抛物线的相切点为
与抛物线的相切点为![]() ,又
,又![]() ,
,
得![]() ,
,![]() .
.
代入直线方程得:![]() ,∴
,∴![]() ……………………………………(4分)
……………………………………(4分)
所以![]() ,
,![]() . ……………………………………………………(5分)
. ……………………………………………………(5分)
(Ⅱ)由(1)知抛物线![]() 方程为
方程为![]() ,焦点
,焦点![]() . ………………(6分)
. ………………(6分)
设![]() ,由(1)知以
,由(1)知以![]() 为切点的切线
为切点的切线![]() 的方程为
的方程为
![]() . ………………………………………(7分)
. ………………………………………(7分)
令![]() ,得切线
,得切线![]() 交
交![]() 轴的
轴的![]() 点坐标为
点坐标为![]() ……………………(8分)
……………………(8分)
所以![]() ,
,![]() ,
,
∵四边形FAMB是以FA、FB为邻边作平行四边形,
∴![]() , ……………………………………………(9分)
, ……………………………………………(9分)
因为![]() 是定点,所以点
是定点,所以点![]() 在定直线
在定直线![]() 上. ………………………(10分)
上. ………………………(10分)
(Ⅲ)设直线![]() , ………………………………(11分)
, ………………………………(11分)
代入![]() 得
得![]() , ………………………………………(12分)
, ………………………………………(12分)
得![]() , ……………………………(13分)
, ……………………………(13分)
![]() ,………(14分)
,………(14分)
![]() .
.![]() △
△![]() 的面积
的面积![]() 范围是
范围是![]() .…………………………………………(15分)
.…………………………………………(15分)

练习册系列答案
相关题目

 中,底面
中,底面 是矩形,
是矩形, 平面
平面 与平面
与平面 和
和 ,
, ,
, 依次是
依次是 的中点.
的中点. ;
; 与平面
与平面 所成角的正弦值.
所成角的正弦值.
 沿直线EF将
沿直线EF将 翻折成
翻折成 使平面
使平面 平面BEF.
平面BEF. 的余弦值;
的余弦值; 重合,求线段FM的长.
重合,求线段FM的长.
 的池底水平铺设污水净化管道
的池底水平铺设污水净化管道 ,
, 是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口
是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口 的中点,
的中点, 分别落在线段
分别落在线段 上.已知
上.已知 米,
米, 米,记
米,记 .
. 表示为
表示为 的函数,并写出定义域;
的函数,并写出定义域;
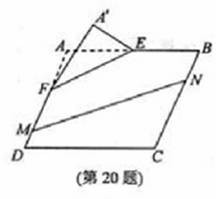 本题满分15分)如图, 在矩形
本题满分15分)如图, 在矩形 中,点
中,点 分别
分别 上,
上, .沿直线
.沿直线
 翻折成
翻折成 ,使平面
,使平面 .
.
 的余弦值;
的余弦值; 分别在线段
分别在线段 上,若沿直线
上,若沿直线 将四
将四 向上翻折,使
向上翻折,使 与
与 重合,求线段
重合,求线段