题目内容

在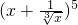 $数学公式$ 的展开式的各项中任取一项，若其系数为奇数时得2分，其系数为偶数时得0分，现从中随机取一项，则其得分的数学期望值是________．

$\text{[math]}$
分析：写出二项展开式的系数，共有6项，写出组合数对应的数字，后面的问题转化为离散型随机变量的概率和期望问题．
解答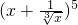： $\text{[math]}$ 的展开式的系数分别是C₅⁰，C₅¹，C₅²，C₅³，C₅⁴，C₅⁵
变化为数字分别是1，5，10，10，5，1
设得分为X则X=0，2
所以 $\text{[math]}$ ， $\text{[math]}$
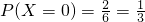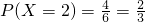
所以其得分的数学期望值是 $\text{[math]}$
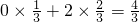
故答案为： $\text{[math]}$
点评：本题考查离散型随机变量的分布列和期望，这种类型是近几年高考题中经常出现的，考查离散型随机变量的分布列和期望，大型考试中理科考试必出的一道问题．

练习册系列答案

小学语文词语手册吉林教育出版社系列答案

初中总复习中考精编系列答案

创新金卷毕业升学系列答案

创新课时训练系列答案

创新学案课时学练测系列答案

创新学习三级训练系列答案

创新与探究系列答案

达标测试卷系列答案

达标训练系列答案

打好基础课堂10分钟系列答案

相关题目

（2011•松江区二模）在(x+

3	x

)5的展开式的各项中任取一项，若其系数为奇数时得2分，其系数为偶数时得0分，现从中随机取一项，则其得分的数学期望值是

3	x2

)n的展开式中各项系数之和为128，在展开式中任取一项，设所取项为有理项的概率为p，则

xpdx=（　　）

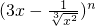如果 $数学公式$ 的展开式中各项系数之和为128，在展开式中任取一项，设所取项为有理项的概率为p，则 $数学公式$ =

A.
$数学公式$
B.
$数学公式$
C.
$数学公式$
D.
$数学公式$

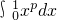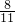
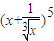的展开式的各项中任取一项，若其系数为奇数时得2分，其系数为偶数时得0分，现从中随机取一项，则其得分的数学期望值是．