题目内容
如果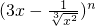 的展开式中各项系数之和为128,在展开式中任取一项,设所取项为有理项的概率为p,则
的展开式中各项系数之和为128,在展开式中任取一项,设所取项为有理项的概率为p,则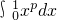 =
=
- A.

- B.

- C.
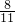
- D.

C
分析:先根据各项系数之和为128求出n;再求出其展开式的通项,得到哪些项为有理项,进而求出p;再求出原函数即可得到答案.
解答:令x=1得,(3-1)n=128?2n=128?n=7.
∴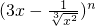 的展开式的通项为:Tr+1=
的展开式的通项为:Tr+1=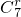 (3x)7-r•
(3x)7-r• =(-1)r•37-r•
=(-1)r•37-r•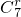 •
•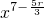 ;
;
当r=0,3,6时,展开式为有理项;
∴p= ;
;
而(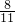 •
•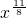 )′=
)′=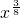 ;
;
∴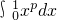 =
=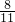
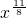
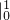 =
=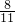 .
.
故选:C
点评:本题主要考察二项式系数的性质以及定积分.是对基础知识的综合考察,属于基础题目,解决本题的关键在于熟练掌握展开式的通项.
分析:先根据各项系数之和为128求出n;再求出其展开式的通项,得到哪些项为有理项,进而求出p;再求出原函数即可得到答案.
解答:令x=1得,(3-1)n=128?2n=128?n=7.
∴
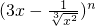 的展开式的通项为:Tr+1=
的展开式的通项为:Tr+1=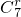 (3x)7-r•
(3x)7-r• =(-1)r•37-r•
=(-1)r•37-r•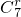 •
•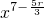 ;
;当r=0,3,6时,展开式为有理项;
∴p=
 ;
;而(
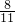 •
•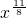 )′=
)′=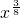 ;
;∴
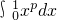 =
=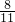
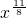
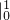 =
=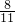 .
.故选:C
点评:本题主要考察二项式系数的性质以及定积分.是对基础知识的综合考察,属于基础题目,解决本题的关键在于熟练掌握展开式的通项.

练习册系列答案
相关题目
 的展开式中各项系数之和为128,则展开式中
的展开式中各项系数之和为128,则展开式中 的系
的系