题目内容
在下列命题中:(1)函数y=tanx在定义域内单调递增;(2)函数y=sinx+arcsinx的最大值为 +sin1;(3)函数y=arccosx-
+sin1;(3)函数y=arccosx- 是偶函数.其中所有错误的命题序号是 .
是偶函数.其中所有错误的命题序号是 .
【答案】分析:根据正切函数的性质判断(1);根据arcsinx表示[- ,
,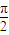 ]上正弦值等于x的一个角,故-
]上正弦值等于x的一个角,故-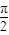 ≤arcsinx≤
≤arcsinx≤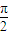 ,从而得到函数y=sinx+arcsinx的最大值;根据偶函数的概念进行判断(3).
,从而得到函数y=sinx+arcsinx的最大值;根据偶函数的概念进行判断(3).
解答:解:对于(1)函数y=tanx在定义域内为增函数;在每一个单调区间是增函数,定义域内不是增函数.故错;
(2)由于 arcsinx表示[-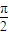 ,
,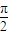 ]上正弦值等于x的一个角,故-
]上正弦值等于x的一个角,故-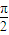 ≤arcsinx≤
≤arcsinx≤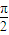 ,
,
∴函数y=sinx+arcsinx的最大值为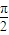 +sin1;正确;
+sin1;正确;
函数y=arccosx-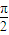 的定义域为[0,π]不关于原点对称,故此函数不是偶函数.
的定义域为[0,π]不关于原点对称,故此函数不是偶函数.
故答案为(1)、(3).
点评:本题考查命题的真假判断与应用,反余弦函数的性质,正切函数的单调性,考查基本概念的掌握程度,是基础题.本小题(2)考查反正弦函数的定义,不等式性质的应用,得到-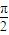 ≤arcsinx≤
≤arcsinx≤ ,是解题的关键.
,是解题的关键.
 ,
,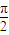 ]上正弦值等于x的一个角,故-
]上正弦值等于x的一个角,故-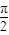 ≤arcsinx≤
≤arcsinx≤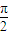 ,从而得到函数y=sinx+arcsinx的最大值;根据偶函数的概念进行判断(3).
,从而得到函数y=sinx+arcsinx的最大值;根据偶函数的概念进行判断(3).解答:解:对于(1)函数y=tanx在定义域内为增函数;在每一个单调区间是增函数,定义域内不是增函数.故错;
(2)由于 arcsinx表示[-
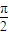 ,
,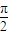 ]上正弦值等于x的一个角,故-
]上正弦值等于x的一个角,故-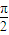 ≤arcsinx≤
≤arcsinx≤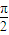 ,
,∴函数y=sinx+arcsinx的最大值为
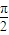 +sin1;正确;
+sin1;正确;函数y=arccosx-
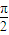 的定义域为[0,π]不关于原点对称,故此函数不是偶函数.
的定义域为[0,π]不关于原点对称,故此函数不是偶函数.故答案为(1)、(3).
点评:本题考查命题的真假判断与应用,反余弦函数的性质,正切函数的单调性,考查基本概念的掌握程度,是基础题.本小题(2)考查反正弦函数的定义,不等式性质的应用,得到-
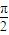 ≤arcsinx≤
≤arcsinx≤ ,是解题的关键.
,是解题的关键. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目