题目内容
设圆过坐标原点，且与直线y=1和y轴均相切，则圆的方程为
x2-2x+y2=0或x2+2x+y2=0
x2-2x+y2=0或x2+2x+y2=0
．分析：由圆过坐标原点，且与直线y=1和y轴均相切，在坐标系中画出相应的图形，根据图形可得所求圆的半径及圆心坐标，由圆心坐标和半径写出圆的标准方程即可．
解答：解：根据题意画出图形，如图所示：
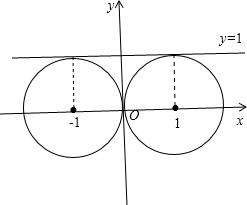
由所求圆过坐标原点，且与直线y=1和y轴均相切，
可得圆的半径为1，圆心坐标为（1，0）或（-1，0），
则所求圆的方程为：（x-1）2+y2=1或（x+1）2+y2=1，即x2-2x+y2=0或x2+2x+y2=0．
故答案为：x2-2x+y2=0或x2+2x+y2=0
由所求圆过坐标原点，且与直线y=1和y轴均相切，
可得圆的半径为1，圆心坐标为（1，0）或（-1，0），
则所求圆的方程为：（x-1）2+y2=1或（x+1）2+y2=1，即x2-2x+y2=0或x2+2x+y2=0．
故答案为：x2-2x+y2=0或x2+2x+y2=0
点评：此题考查了圆的标准方程，以及直线与圆相切的性质，利用了数形结合的思想，其中根据题意画出相应的图形，进而得出所求圆的圆心和半径是解本题的关键．
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
，0）为圆心，1为半径的圆相切，双曲线S的一个顶点A′与点A关于直线y=x对称.设直线l过点A，斜率为k.
；
，求斜率k的值及相应的点B的坐标，如图.
的两条渐进线过坐标原点，且与以点
为圆心，
为半径的圆相且，双曲线的一个顶点
与点
关于直线
对称，设直线
过点
。
时，若双曲线
到直线
，求斜率