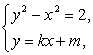题目内容
已知双曲线S的两条渐近线过坐标原点，且与以点A（
，0）为圆心，1为半径的圆相切，双曲线S的一个顶点A′与点A关于直线y=x对称.设直线l过点A，斜率为k.
（1）求双曲线S的方程；
（2）当k=1时，在双曲线S的上支上求点B，使其与直线l的距离为
；
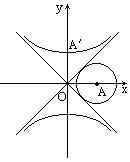
（3）当0≤k＜1时，若双曲线S的上支上有且只有一个点B到直线l的距离为
，求斜率k的值及相应的点B的坐标，如图.
答案：
解析：
解析：
解：（1）由已知可得双曲线的两条渐近线方程为y＝±x，A′（0， 双曲线S的方程为 （2）设B（x， 解得x＝ （3）当0≤k＜1时，双曲线S的上支在直线l的上方，所以B在直线l的上方，设直线l′与直线l：y＝k（x－ 设l′的方程为y=kx+m 由l上的点A到l′的距离为 可知 解得m＝ 因为直线l′在直线l的上方，所以M＝ 由方程组 消去y，得（k2－1）x2＋2mkx＋m2－2＝0， 因为k2≠1，所以 Δ＝4m2k2－4（k2－1）（m2－2）＝4（ 令Δ＝0，由0≤k＜1，解得k＝0，k＝ 当k=0时，m= 此时点B的坐标为（0， 当k＝ |
）．
＝1
）是双曲线S到直线l：y＝x－
的距离为
的点，由点到直线距离公式有
．
，y＝2，即B（
，2）
）平行，两线间的距离为
，且直线l′在直线l的上方，双曲线S的上支上有且仅有一个点B到直线l的距离为
，等价于直线l′与双曲线S的上支有且只有一个公共点.
，
．
（
k）．
（
k）．
－2＋2k2）＝8k（3k－2
）．
．
，解得x=0，y=
．
）；
时，M＝
，解得x＝2
，y＝
．此时点B的坐标为（2
，
）.
练习册系列答案
名师导航单元期末冲刺100分系列答案
名校名卷单元同步训练测试题系列答案
相关题目
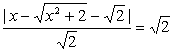，0)为圆心，1为半径的圆相切，双曲线S的一个顶点
与点A关于直线y＝x对称．设直线l过点A，斜率为k．
；
，求斜率k的值及相应的点B的坐标．如图．
，0）为圆心，1为半径的圆相切，双曲线S的一个顶点A′与点A关于直线y=x对称.设直线l过点A，斜率为k.
；
，求斜率k的值及相应的点B的坐标，如图.
，0)为圆心、1为半径的圆相切，双曲线S的一个顶点
与点A关于直线y＝x对称．设直线l过点A，斜率为k．
，0）为圆心，1为半径的圆相切，双曲线S的一个顶点A′与A关于直线y=x对称，设直线l过点A，且斜率为k. 
；
，求斜率k的值及相应的点B的坐标.
.