题目内容
函数f(x)=xcosx在区间[0,2 ]上的零点个数为
]上的零点个数为
 ]上的零点个数为
]上的零点个数为| A.2 | B.3 | C.4 | D.5 |
B
试题分析:考虑到函数y=cosx的零点一定也是函数f(x)的零点,故在区间[0,2π]上y=cosx的零点有2个,结合选项可知结论。
解:因为:∵y=cosx在[0,2π]上有2零点分别为
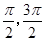 ,那么可知函数y=x的零点有0,因此可知函数函数f(x)=xcosx在区间[0,2
,那么可知函数y=x的零点有0,因此可知函数函数f(x)=xcosx在区间[0,2 ]上的零点个数为3个,选B.
]上的零点个数为3个,选B.点评:本题主要考查了函数零点的意义和判断方法,三角函数的图象和性质,排除法解选择
题,属于基础题。

练习册系列答案
相关题目
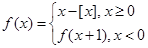 ,其中
,其中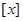 表示不超过
表示不超过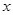 的最大整数,如
的最大整数,如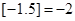 ,
,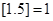 ,若直线
,若直线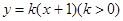 与函数
与函数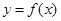 的图象有三个不同的交点,则
的图象有三个不同的交点,则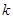 的取值范围是__________.
的取值范围是__________.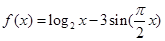 零点的个数是 ( )
零点的个数是 ( )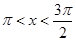 ,则方程
,则方程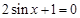 的解
的解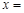 .
. 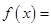 e
e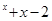 的零点为
的零点为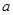 ,函数
,函数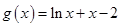
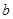 ,则下列不等式中成立的是
,则下列不等式中成立的是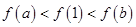
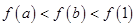
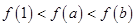
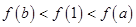
 ,曲线
,曲线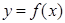 在点
在点 处的切线方程为
处的切线方程为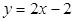 .
.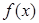 的解析式;
的解析式;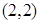 能作几条直线与曲线
能作几条直线与曲线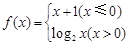 ,则函数
,则函数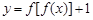 的零点个数是
的零点个数是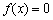 的近似解(精确到0.1),利用计算器得
的近似解(精确到0.1),利用计算器得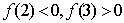 ,
,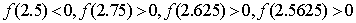 ,则近似解所在区间是( )
,则近似解所在区间是( )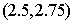
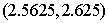
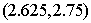
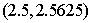
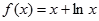 的零点所在的区间为( )
的零点所在的区间为( ) ,1)
,1) )
)