题目内容
设奇函数f（x）的定义域为R，且满足f（x）=-f（x+
），若f（-1）≤1，f（5）=
，则a的取值范围是______．
| 3 |
| 2 |
| 2a-3 |
| a+1 |
由f（x）=-f（x+
），得f（x+
）=-f（x），所以f（x+3）=f（x），即函数f（x）的周期是3．
所以f（5）=f（-1）．
因为f（x）是奇函数，且f（-1）≤1，
所以
≤1，即
≤0，解得1＜a≤4．
即a的取值范围是（1，4]．
故答案为：（1，4]．
| 3 |
| 2 |
| 3 |
| 2 |
所以f（5）=f（-1）．
因为f（x）是奇函数，且f（-1）≤1，
所以
| 2a-3 |
| a+1 |
| a-4 |
| a+1 |
即a的取值范围是（1，4]．
故答案为：（1，4]．
练习册系列答案
备战中考寒假系列答案
相关题目
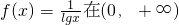是减函数；
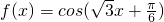，则f（x）+f'（x）是奇函数；
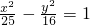的一个焦点到渐近线的距离是5；
是减函数；
，则f（x）+f'（x）是奇函数；
的一个焦点到渐近线的距离是5；