题目内容
选做题：请考生在下列两题中任选一题作答．若两题都做，则按做的第一题评阅计分．本题共5分．（1）．（不等式选讲）若不等式||x-a|-2|＜1的解集是（-2，0）∪（2，4），则实数a=
（2）．（坐标系与参数方程）在极坐标系中，点M（4，
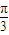）到直线l：ρ（2cosθ+sinθ）=4的距离d= ．
【答案】分析：（1）．由不等式||x-a|-2|＜1解得1+a＜x＜a+3 或a-3＜x＜a-1．再由不等式的解集为（-2，0）∪（2，4），可得a的值．
（2）．先求出点和直线的直角坐标方程，利用点到直线的距离公式求得结果．
解答：解：（1）．由不等式||x-a|-2|＜1可得 1＜|x-a|＜3，故有 1＜x-a＜3，或-3＜x-a＜-1，
解得 1+a＜x＜a+3 或a-3＜x＜a-1．
再由不等式的解集为（-2，0）∪（2，4），可得a=1，
故答案为 1．
（2）．在直角坐标系中，点M（4，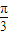
）即（2，2
），
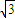直线l：ρ（2cosθ+sinθ）=4即 2x+y-4=0．
故所求的点到直线的距离等于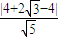
=
，
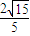故答案为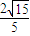
．
点评：本题主要考查绝对值不等式的解法，把极坐标方程化为直角坐标方程的方法，点到直线的距离公式的应用，属于中档题．
（2）．先求出点和直线的直角坐标方程，利用点到直线的距离公式求得结果．
解答：解：（1）．由不等式||x-a|-2|＜1可得 1＜|x-a|＜3，故有 1＜x-a＜3，或-3＜x-a＜-1，
解得 1+a＜x＜a+3 或a-3＜x＜a-1．
再由不等式的解集为（-2，0）∪（2，4），可得a=1，
故答案为 1．
（2）．在直角坐标系中，点M（4，
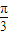）即（2，2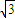），直线l：ρ（2cosθ+sinθ）=4即 2x+y-4=0．
故所求的点到直线的距离等于
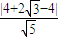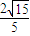=，故答案为
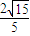．点评：本题主要考查绝对值不等式的解法，把极坐标方程化为直角坐标方程的方法，点到直线的距离公式的应用，属于中档题．
练习册系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
相关题目
选做题：请考生在下列两题中任选一题作答，若两题都做，则按所做的第一题评阅计分．