题目内容
 长方体 ABCD-A1B1C1D1中,底面是边长为2的正方形,AA1=4,
长方体 ABCD-A1B1C1D1中,底面是边长为2的正方形,AA1=4,(1)说出BD1与平面ABCD所成角,并求出它的正切值;
(2)指出 二面角D1-AC-D的平面角,并求出它的正切值;
(3)求证:AC⊥BD1.
分析:(1)由长方体的几何特征,我们易得∠D1BD即为BD1与平面ABCD所成角,解Rt△D1BD即可求出BD1与平面ABCD所成角的正切值;
(2)连接BD,交AC于O,易得∠D1OD为二面角D1-AC-D的平面角,解Rt△D1OD即可求出二面角D1-AC-D的平面角的正切值;
(3)由长方体的几何特征,可得DD1⊥AC,DB⊥AC,由线面垂直的判定定理,即可得到AC⊥面BDD1,再由线面垂直的性质,即可得到AC⊥BD1.
(2)连接BD,交AC于O,易得∠D1OD为二面角D1-AC-D的平面角,解Rt△D1OD即可求出二面角D1-AC-D的平面角的正切值;
(3)由长方体的几何特征,可得DD1⊥AC,DB⊥AC,由线面垂直的判定定理,即可得到AC⊥面BDD1,再由线面垂直的性质,即可得到AC⊥BD1.
解答:解:(1)BD1与平面ABCD所成角为∠D1BD,(1分)
在Rt△D1BD中,DD1=4,BD=2
,tan∠D1BD=
=
(3分)
(2)连接BD,交AC于O,∠D1OD为二面角D1-AC-D的平面角,
在Rt△D1OD中,DD1=4,OD=
,tan∠D1OD=
=2
(6分)
(3)长方体ABCD-A1B1C1D1中,
∴DD1⊥面ABCD,∴DD1⊥AC
正方形ABCD中,DB⊥AC
DD1∩DB=D
∴AC⊥面BDD1,
∴AC⊥BD1,(8分)
在Rt△D1BD中,DD1=4,BD=2
| 2 |
| 4 | ||
2
|
| 2 |
(2)连接BD,交AC于O,∠D1OD为二面角D1-AC-D的平面角,
在Rt△D1OD中,DD1=4,OD=
| 2 |
| 4 | ||
|
| 2 |
(3)长方体ABCD-A1B1C1D1中,
∴DD1⊥面ABCD,∴DD1⊥AC
正方形ABCD中,DB⊥AC
DD1∩DB=D
∴AC⊥面BDD1,
∴AC⊥BD1,(8分)
点评:本题考查的知识点是二面角的平面角及求法,直线与平面垂直的判定,直线与平面所成的角,熟练掌握长方体的几何特征,进而分析出BD1与平面ABCD所成角的平面角,分析出二面角D1-AC-D的平面角,将空间线面夹角及二面角问题转化为解三角形问题,是解答本题的关键.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
 (2009•青浦区二模)(理)在长方体ABCD-A'B'C'D'中,AB=2,AD=1,AA'=1.
(2009•青浦区二模)(理)在长方体ABCD-A'B'C'D'中,AB=2,AD=1,AA'=1.求:
(1)顶点D'到平面B'AC的距离;
(2)二面角B-AC-B'的大小.(结果用反三角函数值表示)
AA′是长方体ABCD-A′B′C′D′的一条棱,这个长方体中与AA′垂直的棱共( )条.
| A、4 | B、6 | C、8 | D、10 |
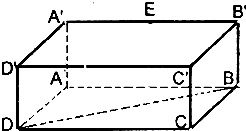 已知长方体ABCD-A′B′C′D′,AB=2,AA′=1,直线BD与平面AA′B′B所成角为30°,E为A′B′的中点.
已知长方体ABCD-A′B′C′D′,AB=2,AA′=1,直线BD与平面AA′B′B所成角为30°,E为A′B′的中点. 如图,已知长方体ABCD-A′B′C′D′中,AB=2
如图,已知长方体ABCD-A′B′C′D′中,AB=2