题目内容
AA′是长方体ABCD-A′B′C′D′的一条棱,这个长方体中与AA′垂直的棱共( )条.
| A、4 | B、6 | C、8 | D、10 |
分析:作出长方体ABCD-A′B′C′D′的图形,利用线面垂直的性质即可求得答案.
解答:解:作出长方体ABCD-A′B′C′D′的图形如下:
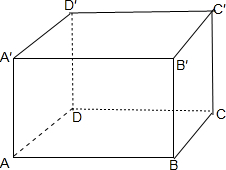
依题意,AA′⊥底面ABCD,AA′⊥平面A′B′C′D′,
∴AA′垂直于底面ABCD中的4条棱AB、BC、CD、DA;
同理可知,AA′垂直于上底面中的4条棱A′B′、B′C′、C′D′、D′A′,
∴这个长方体中与AA′垂直的棱共有8条,
故选:C.

依题意,AA′⊥底面ABCD,AA′⊥平面A′B′C′D′,
∴AA′垂直于底面ABCD中的4条棱AB、BC、CD、DA;
同理可知,AA′垂直于上底面中的4条棱A′B′、B′C′、C′D′、D′A′,
∴这个长方体中与AA′垂直的棱共有8条,
故选:C.
点评:本题考查线面垂直的性质,考查作图能力,属于中档题.

练习册系列答案
相关题目
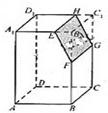 3、如图,若Ω是长方体ABCD-A1B1C1D1被平面EFGH截去几何体EFGHB1C1后得到的几何体,其中E为线段A1B1上异于B1的点,F为线段BB1上异于B1的点,且EH∥A1D1,则下列结论中不正确的是( )
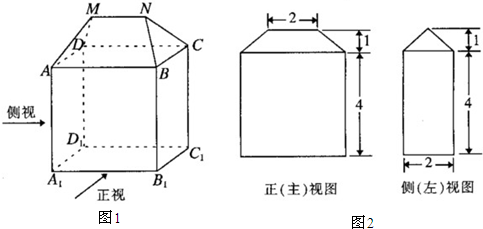
3、如图,若Ω是长方体ABCD-A1B1C1D1被平面EFGH截去几何体EFGHB1C1后得到的几何体,其中E为线段A1B1上异于B1的点,F为线段BB1上异于B1的点,且EH∥A1D1,则下列结论中不正确的是( ) 如图所示为某几何体的直观图和三视图,上半部分是四棱锥P-EFGH,下半部分是长方体ABCD-EFGH.
如图所示为某几何体的直观图和三视图,上半部分是四棱锥P-EFGH,下半部分是长方体ABCD-EFGH.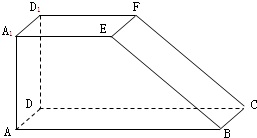 如图是长方体ABCD-A1B1C1D1被一个平面截去一部分后得到的几何体ABCD-A1EFD1,其中EF∥BC,且AB=2AA1=2A1D1=2A1E.
如图是长方体ABCD-A1B1C1D1被一个平面截去一部分后得到的几何体ABCD-A1EFD1,其中EF∥BC,且AB=2AA1=2A1D1=2A1E.