题目内容
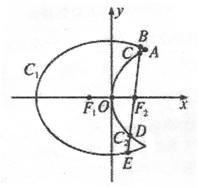
如图,曲线C1是以原点O为中心,F1、F2为焦点的椭圆的一部分,曲线C2是以原点O为顶点,F2为焦点的抛物线的一部分,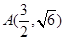 是曲线C1和C2的交点.
是曲线C1和C2的交点.
(Ⅰ)求曲线C1和C2所在的椭圆和抛物线的方程;
(Ⅱ)过F2作一条与x轴不垂直的直线,分别与曲线C1、C2依次交于B、C、D、E四点,若G为CD中点,H为BE中点,问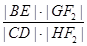 是否为定值,若是,求出定值;若不是,请说明理由.
是否为定值,若是,求出定值;若不是,请说明理由.
【答案】
(Ⅰ)
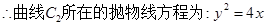 ……………2分
……………2分
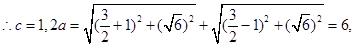
 ……………4分
……………4分
(Ⅱ)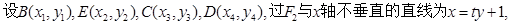
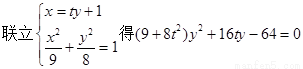
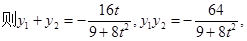 ……………6分
……………6分
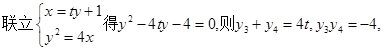 ……………8分
……………8分
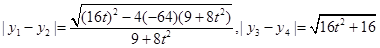
 ……………12分
……………12分
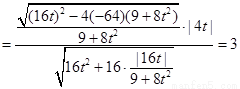

【解析】(1)先根据抛物线过点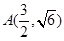 求出方程,然后由定义求2a,写出椭圆方程;(2)设直线方程
求出方程,然后由定义求2a,写出椭圆方程;(2)设直线方程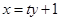 ,与椭圆方程联立,得到
,与椭圆方程联立,得到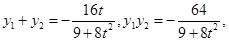
 转化为
转化为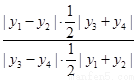 来判断。
来判断。

练习册系列答案
相关题目
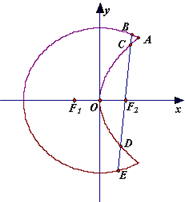 如图,曲线C1是以原点O为中心、F1,F2为焦点的椭圆的一部分,曲线C2是以O为顶点、F2为焦点的抛物线的一部分,A是曲线C1和C2的交点且∠AF2F1为钝角,若|AF1|=
如图,曲线C1是以原点O为中心、F1,F2为焦点的椭圆的一部分,曲线C2是以O为顶点、F2为焦点的抛物线的一部分,A是曲线C1和C2的交点且∠AF2F1为钝角,若|AF1|=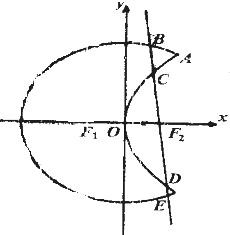 曲线C1是以原点O为中心,F1,F2为焦点的椭圆的一部分,曲线C2是以O为顶点,F2(1,0)为焦点的抛物线的一部分,
曲线C1是以原点O为中心,F1,F2为焦点的椭圆的一部分,曲线C2是以O为顶点,F2(1,0)为焦点的抛物线的一部分,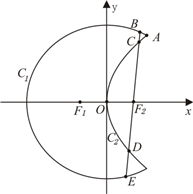 如图,曲线C1是以原点O为中心、F1,F2为焦点的椭圆的一部分,曲线C2是以O为顶点、F2为焦点的抛物线的一部分,A是曲线C1和C2的交点,曲线C1的离心率为
如图,曲线C1是以原点O为中心、F1,F2为焦点的椭圆的一部分,曲线C2是以O为顶点、F2为焦点的抛物线的一部分,A是曲线C1和C2的交点,曲线C1的离心率为 (2012•孝感模拟)如图,曲线C1是以原点O为中心,F1,F2为焦点的椭圆的一部分.曲线C2是以O为顶点,F2为焦点的抛物线的一部分,A是曲线C1和C2的交点且∠AF2F1为钝角,若|AF1|=
(2012•孝感模拟)如图,曲线C1是以原点O为中心,F1,F2为焦点的椭圆的一部分.曲线C2是以O为顶点,F2为焦点的抛物线的一部分,A是曲线C1和C2的交点且∠AF2F1为钝角,若|AF1|= 如图,曲线C1是以原点O为中心,F1、F2为焦点的椭圆的一部分,曲线C2是以原点O为顶点,F2为焦点的抛物线的一部分,
如图,曲线C1是以原点O为中心,F1、F2为焦点的椭圆的一部分,曲线C2是以原点O为顶点,F2为焦点的抛物线的一部分,