Question

已知△ABC中，∠A、∠B、∠C所对的边分别为a、b、c，且a＞c＞b成等差数列，|AB|＝2，求顶点C的轨迹．

Answer 1

答案：
解析：

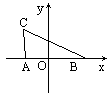
解：以直线AB为x轴，线段AB的中点为原点，建立平面直角坐标系． 　　则A(－1，0)，B(1，0)． 　　设C(x，y) 　　∵a、c、b成等差数列，∴2c＝a＋b， 　　即2|AB|＝|CB|＋|CA|．∴＋＝4． 　　化简整理得3x2＋4y2＝12．即＋＝1． 　　又∵△ABC中，点C不能与A、B共线．∴y≠0． 　　且a＞c＞b，即|CB|＞|CA|．∴x＜0． 　　故顶点C的轨迹为中心在原点，长轴长为4，焦点为A、B的椭圆在y轴左半部分的曲线且去掉点(－2，0)． 　　分析：根据求曲线方程的一般步骤求解．但需注意：(1)完备性；(2)所求为顶点C的轨迹，需指出曲线的形状、特征．