题目内容
方程2x2+mx+n=0有实根，且2、m、n为等差数列的前三项，求该数列公差的取值范围.
答案：
解析：
解析：
设数列的公差为d，则m=2+d，n=2+2d. 由于方程2x2+mx+n=0有实根，得 △=m2－4×2n≥0，即 (2+d)2－8(2+2d) ≥0， 整理，得d2－12d－12≥0. 解得d≤6－4 ∴d∈(－∞，6－4
|
.
∪
6+4
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
(其中i是虚数单位)是实系数方程2x2－mx＋n＝0的一个根，求|m＋ni|的值．
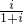（其中i是虚数单位）是实系数方程2x2-mx+n=0的一个根，求|m+ni|的值．