题目内容
(08年丰台区统一练习一理)(13分)
已知如图(1),正三角形ABC的边长为2a,CD是AB边上的高,
E、F分别是AC和BC边上的点,且满足![]() ,现将△ABC
,现将△ABC
沿CD翻折成直二面角A-DC-B,如图(2).
(Ⅰ) 试判断翻折后直线AB与平面DEF的位置关系,并说明理由;
(Ⅱ) 求二面角B-AC-D的大小;
(Ⅲ) 若异面直线AB与DE所成角的余弦值为![]() ,求k的值.
,求k的值.
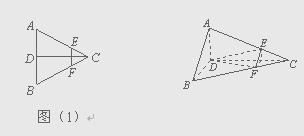
解析:(Ⅰ) AB∥平面DEF. 在△ABC中,
∵ E、F分别是AC、BC上的点,且满足![]() ,
,
∴ AB∥EF.
∵ AB![]() 平面DEF,EF
平面DEF,EF![]() 平面DEF,∴ AB∥平面DEF. …………… 3分
平面DEF,∴ AB∥平面DEF. …………… 3分
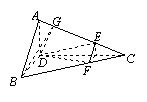
(Ⅱ)过D点作DG⊥AC于G,连结BG,
∵ AD⊥CD, BD⊥CD,
∴ ∠ADB是二面角A-CD-B的平面角.
∴ ∠ADB=![]() , 即BD⊥AD.
, 即BD⊥AD.
∴ BD⊥平面ADC. ∴ BD⊥AC.
∴ AC⊥平面BGD. ∴ BG⊥AC .
∴ ∠BGD是二面角B-AC-D的平面角. ……………………………… 5分
在ADC中,AD=a, DC=![]() , AC=2a,
, AC=2a,
∴ ![]() .
.
在Rt△BDG中,![]() .
.
∴ ![]() .
.
即二面角B-AC-D的大小为![]() .………………………………… 8分
.………………………………… 8分
(Ⅲ)∵ AB∥EF, ∴ ∠DEF(或其补角)是异面直线AB与DE所成的角.… 9分
∵ ![]() ,∴
,∴ ![]() .
.
又DC=![]() ,
, ![]() ,
,
∴![]()
![]()
![]() ………………… 11分
………………… 11分
∴ ![]() .
.
∴ ![]() . 解得
. 解得 ![]() .…………………… 13分
.…………………… 13分

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目