题目内容
已知等差数列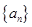 的公差
的公差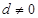 ,若
,若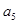 、
、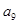 、
、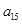 成等比数列,那么
成等比数列,那么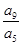 等于 ( )
等于 ( )
A.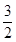 | B.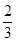 | C.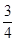 | D.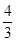 |
A
解析试题分析:∵a5,a9,a15成等比数列,∴a92=a5•a15,即结合等差数列的通项公式表达式得到,
(a1+8d)2=(a1+4d)(a1+14d),整理得:2a1d=8d2,由d≠0,解得:4d=a1,故可知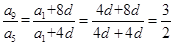 ,故可知选A.
,故可知选A.
考点:本题主要考查了等比数列的性质,以及等比数列的通项公式。
点评:熟练掌握性质及通项公式是解本题的关键.同时利用了等差数列的通项公式表示等比数列的项的关系这也是一个计算易出问题的地方。

练习册系列答案
相关题目
在等差数列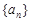 中,已知
中,已知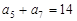 ,则该数列前11项和
,则该数列前11项和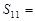
| A.196 | B.132 | C.88 | D.77 |
设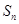 是等差数列{an}的前n项和,
是等差数列{an}的前n项和,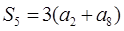 ,则
,则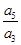 的值为( )
的值为( )
A.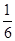 | B.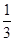 | C.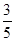 | D.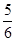 |
设等差数列 的公差不等于0,且其前n项和为
的公差不等于0,且其前n项和为 。若
。若 且
且 成等比数列,则
成等比数列,则
| A.40 | B.54 | C.80 | D.96 |
已知等差数列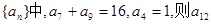 的值是( )
的值是( )
| A.30 | B.15 | C.31 | D.64 |
已知等差数列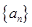 的前
的前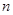 项和为
项和为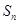 ,
,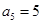 ,
,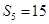 ,则数列
,则数列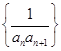 的前100项和为 ( )
的前100项和为 ( )
A.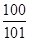 | B.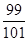 | C.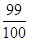 | D. |
等差数列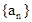 中,已知前15项的和
中,已知前15项的和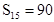 ,则
,则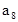 等于( )
等于( )
A.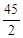 | B.6 | C.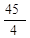 | D.12 |
数列 的
的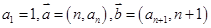 ,且
,且 ,则
,则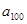 = ( )
= ( )
A.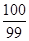 | B.—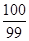 | C.100 | D.—100 |
 的前10项中,所有偶数项、所有奇数项之和分别为55和45,则它的首项
的前10项中,所有偶数项、所有奇数项之和分别为55和45,则它的首项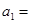 _______。
_______。