题目内容
已知等差数列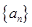 的前
的前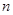 项和为
项和为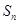 ,
,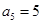 ,
,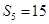 ,则数列
,则数列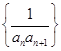 的前100项和为 ( )
的前100项和为 ( )
A.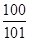 | B.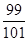 | C.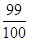 | D. |
A
解析试题分析:利用等差数列通项公式、性质、前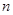 项和公式及裂项相消求和法求解
项和公式及裂项相消求和法求解
方法一
设等差数列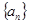 的首项为
的首项为 ,公差为
,公差为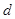 .
. 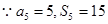
所以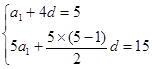 ,所以
,所以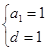 ,所以
,所以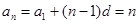
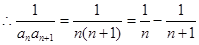 ,所以数列
,所以数列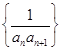 的前100项的和为
的前100项的和为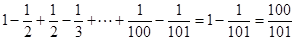
方法二
设等差数列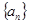 的首项为
的首项为 ,公差为
,公差为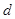 .
.
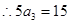
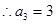 ,又
,又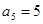
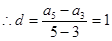
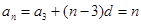 下同方法一略
下同方法一略
考点:本小题主要考查了等差数列通项公式及性质、前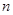 项和公式及裂项相消求和法,考查了方程思想以及运算求解能力。
项和公式及裂项相消求和法,考查了方程思想以及运算求解能力。
点评:解决此类问题的关键是掌握等差数列通项公式及性质、前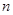 项和公式及裂项相消求和法,并能熟练应用。方法一属于通性通法,便于学生掌握。方法二属于技巧型便于计算,但需要准确掌握等差数列的常用性质,难度适中。
项和公式及裂项相消求和法,并能熟练应用。方法一属于通性通法,便于学生掌握。方法二属于技巧型便于计算,但需要准确掌握等差数列的常用性质,难度适中。

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
已知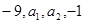 成等差数列,
成等差数列,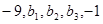 成等比数列 ,则
成等比数列 ,则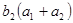 等于( )
等于( )
| A.30 | B.-30 | C.±30 | D.15 |
已知等差数列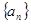 的公差为2,若
的公差为2,若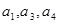 成等比数列, 则
成等比数列, 则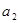 =( )
=( )
| A.–4 | B.–6 | C.–8 | D.–10 |
已知等差数列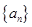 的公差
的公差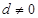 ,若
,若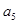 、
、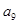 、
、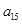 成等比数列,那么
成等比数列,那么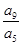 等于 ( )
等于 ( )
A.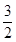 | B.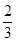 | C.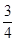 | D.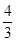 |
在等差数列 中,已知
中,已知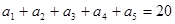 ,那么
,那么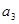 =
=
| A.3 | B.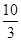 | C.4 | D.5 |
已知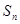 为等差数列
为等差数列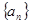 的前
的前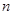 项的和,
项的和,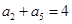 ,
,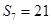 ,则
,则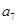 的值为( )
的值为( )
| A.6 | B.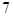 | C.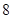 | D.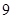 |
若两个等差数列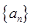 和
和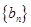 的前
的前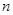 项和分别是
项和分别是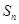 和
和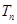 ,已知
,已知 =
=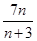 ,则
,则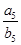 =( )
=( )
| A.7 | B. | C.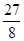 | D. |
已知各项均为正数的等比数列{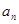 },
},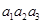 =5,
=5,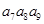 =10,则
=10,则
 =( )
=( )
A.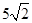 | B.7 | C.6 | D.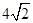 |
设等差数列 的前
的前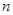 项和为
项和为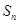 ,若
,若 ,
,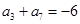 ,则当
,则当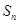 取最小值时,
取最小值时,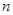 等于 ( )
等于 ( )
| A.8 | B.7 | C.6 | D.9 |