题目内容
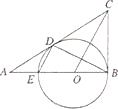21、已知：如图，在△ABC中，∠ABC=90°，O是AB上一点，以O为圆心，OB为半径的圆与AB交于点E，与AC切于点D，连接DB、DE、OC．若AD=2，AE=1，求CD的长．分析：先由切割线定理AD2=AE•AB，结合已知条件求得AB的值，再设CD=x，在直角三角形ABC中利用勾股定理列方程求解即可．
解答：解：因为圆O与AC切于点D，由切割线定理得
AD2=AE•AB，即22=AB，∴AB=4．（4分）
设CD=x，则CB=x，
在直角三角形ABC中，x2+42=（x+2）2，
解之得x=3．（10分）
AD2=AE•AB，即22=AB，∴AB=4．（4分）
设CD=x，则CB=x，
在直角三角形ABC中，x2+42=（x+2）2，
解之得x=3．（10分）
点评：本题利用了弦切角定理和与圆有关的比例线段的性质，三角形勾股定理求解．
练习册系列答案
相关题目
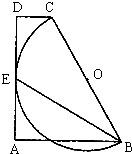已知：如图，在直角梯形ABCD中，AB∥CD，AD⊥AB，垂足为A，以腰BC为直径的半圆O切AD于点E，连接BE，若BC=6，∠EBC=30°，则梯形ABCD的面积为
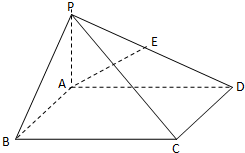已知：如图，在四棱锥P-ABCD中，底面ABCD是矩形，PA⊥平面ABCD，PA=AB=1，BC=2．
已知：如图，在四棱锥P-ABCD中，底面ABCD是矩形，PA⊥平面ABCD，PA=AB=1，BC=2．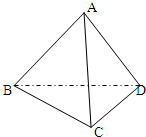
（文科做）已知：如图，在空间四边形ABCD中，AB⊥CD且AC⊥BD，求证：AD⊥BC．