题目内容
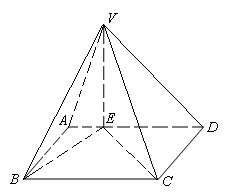
如图,已知四棱锥 ,底面
,底面 是平行四边形,点
是平行四边形,点 在平面
在平面 上的射影
上的射影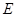 在
在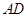 边上,且
边上,且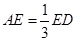 ,
,
 .
.
(Ⅰ)设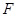 是
是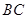 的中点,求异面直线
的中点,求异面直线 与
与 所成角的余弦值;
所成角的余弦值;
(Ⅱ)设点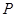 在棱
在棱 上,且
上,且 .求
.求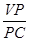 的值.
的值.
(Ⅰ)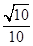 ;(Ⅱ)
;(Ⅱ) .
.
解析试题分析:(Ⅰ)在平面 内,过
内,过 作
作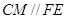 交
交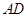 与
与 ,连接
,连接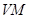 ,则
,则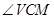 或其补角即为异面直线
或其补角即为异面直线 与
与 所成角.然后在
所成角.然后在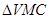 中求出
中求出 与
与 所成角的余弦值为
所成角的余弦值为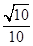 ;(Ⅱ)此问关键是要抓住
;(Ⅱ)此问关键是要抓住 这一条件,结合题目所给条件建立
这一条件,结合题目所给条件建立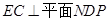 后进行求解.
后进行求解.
试题解析:
(Ⅰ)在平面 内,过
内,过 作
作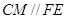 交
交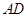 与
与 ,连接
,连接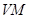 ,则
,则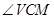 或其补角即为异面直线
或其补角即为异面直线 与
与 所成角.
所成角.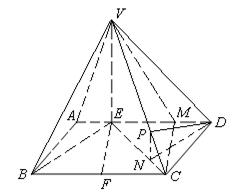
在△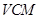 中,
中,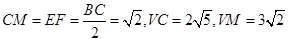 ,
,
由余弦定理得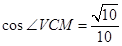 ,
,
故异面直线 与
与 所成角的余弦值为
所成角的余弦值为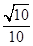 .
.
(Ⅱ)在平面 内,过
内,过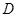 作
作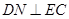 交
交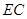 与
与 ,连接
,连接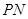 ,
,
∵ ,∴
,∴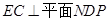 ,∴
,∴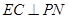 .
.
又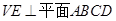 ,故
,故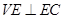 ,故在平面
,故在平面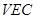 中可知
中可知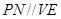 ,
,
故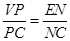 ,又
,又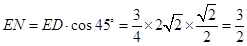 ,
,
故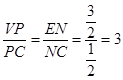 .
.
考点:线与线所成角;线面垂直.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
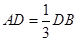 ,点C为圆O上一点,且
,点C为圆O上一点,且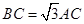 .点P在圆O所在平面上的正投影为点D,PD=DB.
.点P在圆O所在平面上的正投影为点D,PD=DB.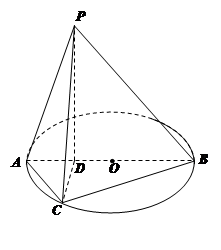
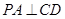 ;
;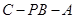 的余弦值.
的余弦值.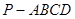 中,底面为直角梯形,
中,底面为直角梯形,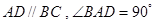 ,
,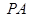 垂直于底面
垂直于底面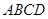 ,
,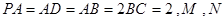 分别为
分别为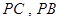 的中点.
的中点.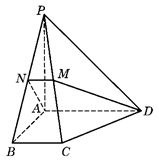
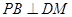 ;
;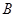 到平面
到平面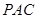 的距离.
的距离. 中,底面
中,底面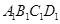 是正方形,
是正方形, 是
是 的中点,
的中点,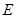 是棱
是棱 上任意一点.
上任意一点.
 ;
; ,求
,求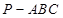 中,
中,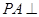 平面
平面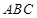 ,
,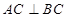 ,
, 为侧棱
为侧棱 上一点,它的正(主)视图和侧(左)视图如图所示.
上一点,它的正(主)视图和侧(左)视图如图所示.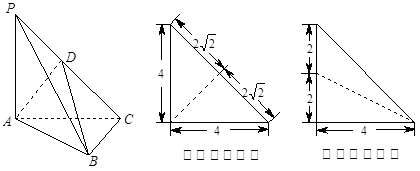
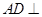 平面
平面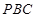 ;
;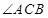 的平分线上确定一点
的平分线上确定一点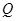 ,使得
,使得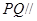 平面
平面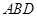 ,并求此时
,并求此时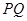 的长.
的长.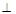 平面CDE,AE=3.
平面CDE,AE=3.
 为
为 的中点,求证:
的中点,求证: 平面
平面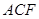 ;
;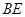 与平面
与平面 所成角的正弦值.
所成角的正弦值. 中,
中,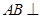 平面
平面 ,
,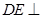 平面
平面
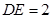 ,
,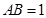 ,
, 为
为 的中点.
的中点.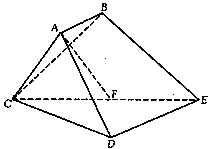
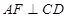 ;
;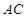 与平面
与平面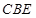 所成角的余弦值的大小.
所成角的余弦值的大小.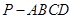 中,底面
中,底面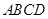 为菱形,
为菱形,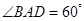 ,
,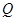 为
为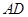 的中点.
的中点.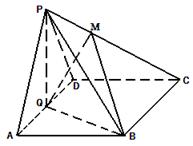
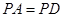 ,求证:平面
,求证:平面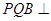 平面
平面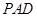 ;
;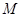 在线段
在线段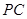 上,
上,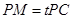 ,试确定
,试确定 的值,使
的值,使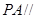 平面
平面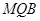 .
.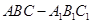 中, D是 AC的中点。
中, D是 AC的中点。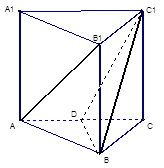
 //平面
//平面