题目内容
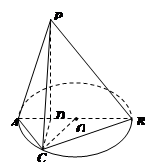
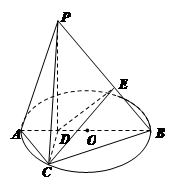
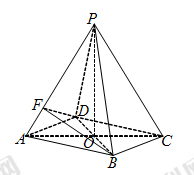
如图所示,已知AB为圆O的直径,点D为线段AB上一点,且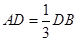 ,点C为圆O上一点,且
,点C为圆O上一点,且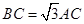 .点P在圆O所在平面上的正投影为点D,PD=DB.
.点P在圆O所在平面上的正投影为点D,PD=DB.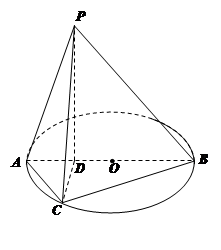
(1)求证: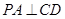 ;
;
(2)求二面角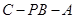 的余弦值.
的余弦值.
(1)证明见解析;(2)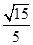 .
.
解析试题分析:(1)先利用平面几何知识与线面垂直的性质证线线垂直,由线线垂直得到线面垂直,再由线面垂直得到线线垂直;(2)作出二面角的平面角,证明符合二面角的定义,再在三角形中求二面角的平面角,从而求出所求的二面角.
试题解析:(1)如图,连接 ,
,
由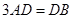 知,点
知,点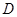 为
为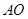 的中点,
的中点,
又∵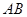 为圆
为圆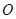 的直径,
的直径,
∴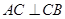 ,
,
由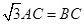 知,
知,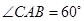 ,
,
∴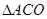 为等边三角形,从而
为等边三角形,从而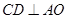 .
.
∵点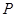 在圆
在圆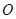 所在平面上的正投影为点
所在平面上的正投影为点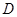 ,
,
∴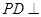 平面
平面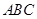 ,又
,又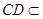 平面
平面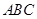 ,
,
∴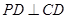 ,
,
由 得,
得,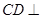 平面
平面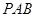 ,
,
又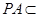 平面
平面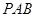 ,
,
∴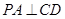 .
.
(2)方法1:(综合法)如图,过点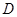 作
作 ,垂足为
,垂足为 ,连接
,连接 ,
, 
由(1)知 平面
平面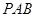 ,
,
又∵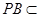 平面
平面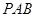 ,
,
∴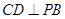 ,
,
又∵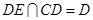 ,
,
∴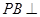 平面
平面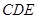 ,
,
又∵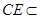 平面
平面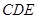 ,
,
∴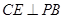 ,
,
∴ 为二面角
为二面角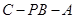 的平面角.
的平面角.
由(Ⅰ)可知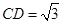 ,
,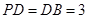 ,
,
∴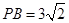 ,则
,则 ,
,
∴在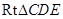 中,
中,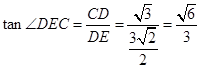 ,
,
∴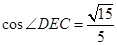 ,即二面角
,即二面角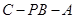 的余弦值为
的余弦值为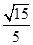 .
.
方法2:(坐标法)以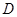 为原点,
为原点,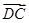 、
、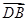 和
和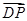 的方向分别为
的方向分别为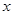 轴、
轴、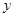 轴和
轴和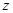 轴的正向,建立如图所示的空间直角坐标系,
轴的正向,建立如图所示的空间直角坐标系,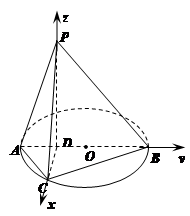
设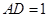 ,由
,由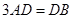 ,
,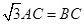 得,
得,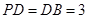 ,
,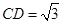 ,
,
∴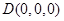 ,
,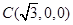 ,
,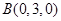 ,
,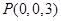 ,
,
∴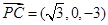 ,
,
练习册系列答案
相关题目
 的直径
的直径 ,点
,点 、
、 为
为 ,
,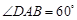 ,
, 为弧
为弧 的中点.将
的中点.将 折起,使两个半圆所在平面互相垂直(如图2).
折起,使两个半圆所在平面互相垂直(如图2).
 ;
; 上是否存在点
上是否存在点 ,使得
,使得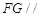 平面
平面 ?若存在,试指出点
?若存在,试指出点 的正弦值.
的正弦值. 的侧棱长和底面边长均为2,
的侧棱长和底面边长均为2, 在底面ABC内的射影O为底面△ABC的中心,如图所示:
在底面ABC内的射影O为底面△ABC的中心,如图所示:
 ,求异面直线
,求异面直线 与
与 、
、 ,求三棱锥C1-BCA1的体积.
,求三棱锥C1-BCA1的体积.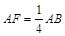 .
.
 中,底面四边形
中,底面四边形 是菱形,
是菱形, ,
, 是边长为2的等边三角形,
是边长为2的等边三角形, ,
,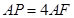 .
.
 底面
底面 与平面
与平面 所成角的大小;
所成角的大小; 上是否存在一点
上是否存在一点 ,使得
,使得 ∥平面
∥平面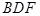 ?如果存在,求
?如果存在,求 的值,如果不存在,请说明理由.
的值,如果不存在,请说明理由. 面ABEF,且DA=1,AB//EF,
面ABEF,且DA=1,AB//EF,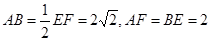 ,P、Q、M分别为AE、BD、EF的中点.
,P、Q、M分别为AE、BD、EF的中点.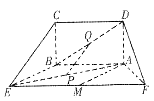

 底面ABCD,SA=AD,点M是SD的中点,AN
底面ABCD,SA=AD,点M是SD的中点,AN
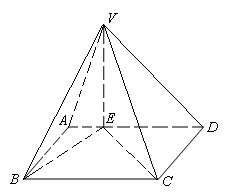
 ,底面
,底面 是平行四边形,点
是平行四边形,点 在平面
在平面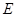 在
在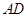 边上,且
边上,且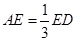 ,
,
 .
.
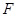 是
是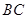 的中点,求异面直线
的中点,求异面直线 与
与 所成角的余弦值;
所成角的余弦值;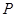 在棱
在棱 .求
.求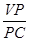 的值.
的值.