题目内容
已知双曲线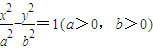 的左、右焦点分别为F1,F2,P是准线上一点,且PF1⊥PF2,|PF1|•|PF2|=4ab,则双曲线的离心率是( )
的左、右焦点分别为F1,F2,P是准线上一点,且PF1⊥PF2,|PF1|•|PF2|=4ab,则双曲线的离心率是( )A.

B.
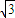
C.2
D.3
【答案】分析:由PF1⊥PF2,|PF1|•|PF2|=4ab可知:PF1|•|PF2|=|F1F2|•|PA|,导出 ,由此能够求出双曲线的离心率.
,由此能够求出双曲线的离心率.
解答:解:设准线与x轴交于A点.在Rt△PF1F2中,
∵|PF1|•|PF2|=|F1F2|•|PA|,
∴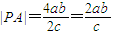 ,
,
又∵|PA|2=|F1A|•|F2A|,
∴ ,
,
化简得c2=3a2,
∴ .
.
故选答案B
点评:本题考查双曲线的离心率的求法解三角形的相关知识.解题时不能联系三角形的有关知识,找不到解题方法而乱选.双曲线的离心率的求法是解析几何的一个重点,且方法较多,要善于总结各种方法,灵活应用
 ,由此能够求出双曲线的离心率.
,由此能够求出双曲线的离心率.解答:解:设准线与x轴交于A点.在Rt△PF1F2中,
∵|PF1|•|PF2|=|F1F2|•|PA|,
∴
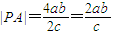 ,
,又∵|PA|2=|F1A|•|F2A|,
∴
 ,
,化简得c2=3a2,
∴
 .
.故选答案B
点评:本题考查双曲线的离心率的求法解三角形的相关知识.解题时不能联系三角形的有关知识,找不到解题方法而乱选.双曲线的离心率的求法是解析几何的一个重点,且方法较多,要善于总结各种方法,灵活应用

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
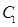 的方程为
的方程为 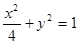 ,双曲线
,双曲线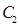 的左、右焦
的左、右焦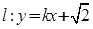 与双曲线C2恒有两个不同的交点A和B,求
与双曲线C2恒有两个不同的交点A和B,求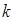 的范围。
的范围。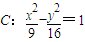 的左、右焦 点分别为F1、F2,P为C的右支上一点,且
的左、右焦 点分别为F1、F2,P为C的右支上一点,且 的面积等于 .
的面积等于 .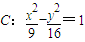 的左、右焦 点分别为F1、F2,P为C的右支上一点,且
的左、右焦 点分别为F1、F2,P为C的右支上一点,且 的面积等于 .
的面积等于 .