题目内容
(1)已知S=| A | 1 1 |
| A | 2 2 |
| A | 2014 2014 |
(2)求和S=
| C | 2 5 |
| C | 2 6 |
| C | 2 7 |
| C | 2 2014 |
分析:(1)展开几个排列数看出规律,前四个没有特殊的结果,而从第五项开始每一个排列数的结果都是个位数是0,得到结论;
(2)利用组合数的性质,即可得出结论.
(2)利用组合数的性质,即可得出结论.
解答:解:(Ⅰ)A11=1,A22=2,A33=6,A44=24,
而A55,A66,…,A100100中都含有5和至少一个偶数,
所以S的后两位由
+
+…+
确定,故个位数字为3,十位数字为1
所以ab=3
(Ⅱ)S=
+
+
+…+
=
+
+
+
+…+
-
=
+
+
+…+
-
=…=
-
.
而A55,A66,…,A100100中都含有5和至少一个偶数,
所以S的后两位由
| A | 1 1 |
| A | 2 2 |
| A | 9 9 |
所以ab=3
(Ⅱ)S=
| C | 2 5 |
| C | 2 6 |
| C | 2 7 |
| C | 2 2014 |
| C | 3 5 |
| C | 2 5 |
| C | 2 6 |
| C | 2 7 |
| C | 2 2014 |
| C | 3 5 |
=
| C | 3 6 |
| C | 2 6 |
| C | 2 7 |
| C | 2 2014 |
| C | 3 5 |
| C | 3 2015 |
| C | 3 5 |
点评:本题考查排列数、组合数的性质和应用,解题时要注意总结规律.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
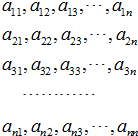 如图,由n2个数组成的方阵中,自左向右每一行都构成等差数列,设第1,2,…,n行的公差依次为d1,d2,…,dn.方阵中自上而下每一列组成公比均相同的等比数列,已知a11=1,a12=a21=2.
如图,由n2个数组成的方阵中,自左向右每一行都构成等差数列,设第1,2,…,n行的公差依次为d1,d2,…,dn.方阵中自上而下每一列组成公比均相同的等比数列,已知a11=1,a12=a21=2.