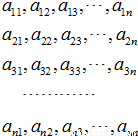Question

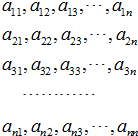如图，由n²个数组成的方阵中，自左向右每一行都构成等差数列，设第1，2，…，n行的公差依次为d₁，d₂，…，d_n．方阵中自上而下每一列组成公比均相同的等比数列，已知a₁₁=1，a₁₂=a₂₁=2．
（1）求d₄及a₄₄的值；
（2）若n=6，求方阵中所有数的和S．

Answer 1

分析：（1）仔细观察图表，由题设条件结合等差和等比数列的性质，即可能求出求出d₄及a₄₄的值．
（2）由图表中的规律，a₁₃=3，a₁₄=4，a₁₅=5，a₁₆=6，设第1列，第2列，…，第6列的和分别为S₁，S₂，S₃，…，S₆从而由已知每一列组成公比为q=2的等比数列，由此利用等比和等差数列的求和公式能求出方阵中所有数的和S．

解答：解：设每一列组成的等比数列的公比为q
（1）q=

a21

a11

=2，a41=a11q3=8，a42=a21q3=16，…（3分）
d₄=a₄₂-a₄₁=8a₄₄=a₄₁+3d₄=32…（6分）
（2）a₁₃=3，a₁₄=4，a₁₅=5，a₁₆=6
设第1列，第2列，…，第6列的和分别为S₁，S₂，S₃，…，S₆
由已知每一列组成公比为q=2的等比数列，
故S=S1+S2+…+S6=

a11(1-26)

1-2

+

a12(1-26)

1-2

+…+

a16(1-26)

1-2

=63(a11+a12+…+a16)=63×

6(1+6)

2

=1323…（12分）

点评：本题考查数列与函数的综合应用，考查推理论证能力，考查等价转化思想，考查计算能力，考查等差数列和等比数列的性质，解题时要注意求和公式的合理运用．