题目内容
【题目】【选做题】在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.请在答卷卡指定区域内作答.解答应写出文字说明、证明过程或演算步骤.
A.选修4—1:几何证明选讲
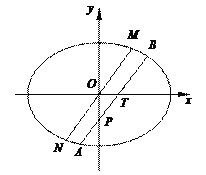
如图,△ABC的顶点A,C在圆O上,B在圆外,线段AB与圆O交于点M.

(1)若BC是圆O的切线,且AB=8,BC=4,求线段AM的长度;
(2)若线段BC与圆O交于另一点N,且AB=2AC,求证:BN=2MN.
B.选修4—2:矩阵与变换
设a,b∈R.若直线l:ax+y-7=0在矩阵A= ![]() 对应的变换作用下,得到的直线为l′:9x+y-91=0.求实数a,b的值.
对应的变换作用下,得到的直线为l′:9x+y-91=0.求实数a,b的值.
C.选修4—4:坐标系与参数方程
在平面直角坐标系xOy中,直线l:  (t为参数),与曲线C:
(t为参数),与曲线C:  (k为参数)交于A,B两点,求线段AB的长.
(k为参数)交于A,B两点,求线段AB的长.
D.选修4—5:不等式选讲
设a≠b,求证:a4+6a2b2+b4>4ab(a2+b2).
【答案】见解析.
试题分析:作差比较,化简得出原式=![]() ,即可作出证明。
,即可作出证明。
试题解析:
证明: a4+6a2b2+b4-4ab(a2+b2)=(a2+b2)2-4ab(a2+b2)+4a2b2
=(a2+b2-2ab)2=(a-b)4.
因为a≠b,所以(a-b)4>0, 所以a4+6a2b2+b4>4ab(a2+b2).
【解析】试题分析:(1)因为![]() 是圆
是圆![]() 的切线,故由切割线定理得
的切线,故由切割线定理得![]() ,设
,设![]() ,列出方程,即可求解
,列出方程,即可求解![]() 的值,得到
的值,得到![]() 的长;
的长;
(2)根据![]() 和
和![]() 相似,列出比例关系式,即可得出证明。
相似,列出比例关系式,即可得出证明。
试题解析:
解:(1)因为BC是圆O的切线,故由切割线定理得BC2=BM·BA.
设AM=t,因为AB=8,BC=4,
所以42=8(8-t),解得t=6 ,即线段AM的长度为6.
(2)因为四边形AMNC为圆内接四边形,所以∠A=∠MNB.又∠B=∠B,所以△BMN∽△BCA,
所以![]() =
=![]() .
.
因为AB=2AC,所以BN=2MN.
B.选修4—2:矩阵与变换
设a,b∈R.若直线l:ax+y-7=0在矩阵A= ![]() 对应的变换作用下,得到的直线为l′:9x+y-91=0.求实数a,b的值.
对应的变换作用下,得到的直线为l′:9x+y-91=0.求实数a,b的值.

【题目】春节期间,“厉行节约,反对浪费”之风悄然吹开,某市通过随机询问100名性别不同的居民是否能做到“光盘”行动,得到如下的列联表:
做不到“光盘” | 能做到“光盘” | |
男 | 45 | 10 |
女 | 30 | 15 |
P(K2≥k) | 0.10 | 0.05 | 0.025 |
k | 2.706 | 3.841 | 5.024 |
附: ![]()
参照附表,得到的正确结论是( )
A.在犯错误的概率不超过l%的前提下,认为“该市居民能否做到‘光盘’与性别有关”
B.在犯错误的概率不超过l%的前提下,认为“该市居民能否做到‘光盘’与性别无关”
C.有90%以上的把握认为“该市居民能否做到‘光盘’与性别有关”
D.有90%以上的把握认为“该市居民能否做到‘光盘’与性别无关”