题目内容
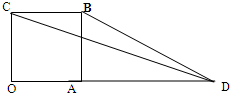 如图,四边形OABC是边长为1的正方形,
如图,四边形OABC是边长为1的正方形,| OD |
| OA |
| OP |
| OC |
| OD |
分析:以OD为x轴,OC为y轴,建立直角坐标系,根据点P为△BCD(含边界)内的一个动点建立不等关系,最后将3y看整体,则x2+9y2表示区域里点到原点距离的平方的几何意义进行求解即可.
解答:解:以OD为x轴,OC为y轴,建立直角坐标系
则C(0,1),D(3,0),B(1,1)
直线CD的方程为x+3y-3=0,直线BD的方程为x+2y-3=0
=x
+y
=(m,n)=(3y,x)
∵点P为△BCD(含边界)内的一个动点
∴
将3y看整体,则x2+9y2表示区域里点到原点距离的平方
当原点到直线3x+y-3=0的距离时x2+9y2取最小值
即d=
∴x2+9y2的最小值等于
故答案为:
则C(0,1),D(3,0),B(1,1)
直线CD的方程为x+3y-3=0,直线BD的方程为x+2y-3=0
| OP |
| OC |
| OD |
∵点P为△BCD(含边界)内的一个动点
∴
|
将3y看整体,则x2+9y2表示区域里点到原点距离的平方
当原点到直线3x+y-3=0的距离时x2+9y2取最小值
即d=
| 3 | ||
|
∴x2+9y2的最小值等于
| 9 |
| 10 |
故答案为:
| 9 |
| 10 |
点评:本题主要考查了向量在几何中的应用,以及利用解析法求解和线性规划的方法求最值,有一定的难度,属于中档题.

练习册系列答案
相关题目

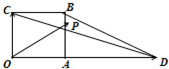 如图,四边形OABC是边长为1的正方形,OD=3,点P为△BCD内(含边界)的动点,设
如图,四边形OABC是边长为1的正方形,OD=3,点P为△BCD内(含边界)的动点,设 如图,四边形OABC是面积为4的正方形,函数
如图,四边形OABC是面积为4的正方形,函数 (2013•文昌模拟)如图,四边形OABC是边长为1的正方形,OD=3,点P为△BCD内(含边界)的动点,设
(2013•文昌模拟)如图,四边形OABC是边长为1的正方形,OD=3,点P为△BCD内(含边界)的动点,设