题目内容
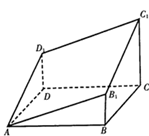
正方体的棱长为 ,由它的互不相邻的四个顶点连线所构成的四面体的体积是( )
,由它的互不相邻的四个顶点连线所构成的四面体的体积是( )
A. | B. | C. | D. |
C
解析试题分析:正方体体积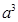 ,正方体四个顶点处三棱锥体积都为
,正方体四个顶点处三棱锥体积都为 ,所以所求体积为
,所以所求体积为
考点:四棱锥体积
点评:正四面体与正方体间的联系:正四面体的边长是正方体的面对角线

练习册系列答案
相关题目
右图是一个几何体的正视图和侧视图。其俯视图是面积为 的矩形。则该几何体的表面积是
的矩形。则该几何体的表面积是
| A.8 | B. |
| C.16 | D. |
四面体的五条棱长都是2,另一条棱长为1,则四面体的体积为( )。
A. | B. | C. | D. |
如图,正方体 的棱长为1,线段
的棱长为1,线段 上有两个动点E,F,且
上有两个动点E,F,且 ,则下列结论中错误的是 ( )
,则下列结论中错误的是 ( )
A. |
B. |
C.三棱锥 的体积为定值 的体积为定值 |
D.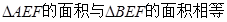 |
一个几何体的底面是正三角形,侧棱垂直于底面,它的三视图及其尺寸如下(单位cm),则该几何体的表面积为( )
A.4(9+2 ) cm2 ) cm2 | B. cm2 cm2 |
C.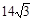 cm2 cm2 | D. cm cm |
各棱长均为 的三棱锥的表面积为
的三棱锥的表面积为
A. | B. | C.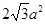 | D. |
正方体 ,棱长为
,棱长为 ,点
,点 到截面
到截面 的距离为( )
的距离为( )
A. | B.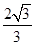 | C. | D. |
从点 出发的三条射线
出发的三条射线 两两成
两两成 角,且分别与球
角,且分别与球 相切于
相切于 三点,若球的体积为
三点,若球的体积为 ,则
,则 两点之间的距离为( )
两点之间的距离为( )
A. | B. | C.1.5 | D.2 |