Question

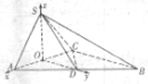已知三棱锥S-ABC中，平面ASC⊥平面ABC，O、D分别为AC、AB的中点，AS=CS=CD=AD=

2

2

AC．
（I）求证：平面ASC⊥平面BCS；
（II）求二面角A-SC-D的余弦值．

Answer 1

分析：（I）根据几何体的结构特征得到SO⊥AC，OD⊥AC，进而利用垂直共线得到BC⊥AC与SO⊥BC，可证明线面垂直，又因为垂线在另一个平面内所以可得面面垂直．
（II）建立坐标系分别求出两个平面的法向量，结合向量的有关运算求出两个向量的夹角，进而得到二面角的余弦值．

解答：解：（I）因为AS=CS=CD=AD=

2

2

AC，O为AC的中点
所以SO⊥AC，OD⊥AC，
又D为AB的中点，所以OD∥BC，所以BC⊥AC．
又因为平面SAC⊥平面ABC，
所以SO⊥平面ABC，所以SO⊥BC．
故可得CB⊥平面SAC．
因为BC?平面BSC，
所以平面ASC⊥平面BSC．
（II）由（I）得SO⊥AC，SO⊥OD，AC⊥OD，所以分别以OA，OD，OS为轴建立如图的空间直角坐标系O-xyz．

设AS=CS=CD=AD=2，则A（

2

，0，0），D（0，

2

，0），C（-

2

，0，0），S（0，0，

2

）
则

CS

=(

2

，0，

2

)，

CD

=(

2

， 

2

，0)，

OD

=(0，

2

，0)．
设

a

=（x，y，z）是平面CDS的法向量，
则

a • CD =0 a • CS =0

即

x+y=0 x+z=0

，
令x=-1得

a

=(-1，1，1)．

OD

为平面ASC的法向量，设二面角A-SC-D为θ，
所以cosθ=

| OD • a |

| OD | • | a |

=

2

2 • 3

=

3

3

即所求角的余弦值为

3

3

．

点评：解决此类问题的关键是熟悉几何体的结构特征，有利于确定线面垂直的条件，也便于建立坐标系利用向量解决二面角的平面角问题．