题目内容
已知函数g(x)在(0,+∞)上是增函数,g(x)=f(|x|).若f(x)=lgx,则g(lgx)>g(1)时x的取值范围是
(0,
)∪(10,+∞)
| 1 |
| 10 |
(0,
)∪(10,+∞)
.| 1 |
| 10 |
分析:据题意知g(x)=lg|x|为偶函数且g(lgx)>g(1),由偶函数的性质可得|lgx|>1,解不等式可求
解答:解:根据题意知g(x)=lg|x|为偶函数
又因为g(lgx)>g(1),且函数y=lgx为(0,+∞)单调递增
∴y=lg|x|在(-∞,0)上单调递减且函数的图象关于y轴对称
所以|lgx|>1,
∴lgx>1或lgx<-1
解得0<x<
或x>10.
故答案:(0,
)∪(10,+∞)
又因为g(lgx)>g(1),且函数y=lgx为(0,+∞)单调递增
∴y=lg|x|在(-∞,0)上单调递减且函数的图象关于y轴对称
所以|lgx|>1,
∴lgx>1或lgx<-1
解得0<x<
| 1 |
| 10 |
故答案:(0,
| 1 |
| 10 |
点评:本题主要考查了偶函数单调性性质的应用,熟记一些常用的结论可以简化基本运算.

练习册系列答案
相关题目
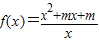 的图象关于点(0,1)对称,求实数m的值;
的图象关于点(0,1)对称,求实数m的值;