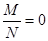题目内容
若函数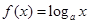
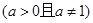 在
在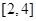 上的最大值与最小值之差为2,则
上的最大值与最小值之差为2,则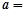 .
.
【答案】
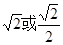 .
.
【解析】
试题分析:因为函数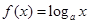
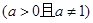 在
在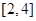 是单调函数,所以其最大值与最小值必在区间端点取到。由最大值与最小值之差为2,得
是单调函数,所以其最大值与最小值必在区间端点取到。由最大值与最小值之差为2,得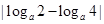 =2,即
=2,即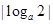 =2,解得a为
=2,解得a为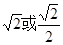 。
。
考点:本题主要考查对数函数的性质。
点评:简单题,利用对数函数是单调函数,建立a的方程。

练习册系列答案
相关题目
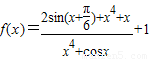 在
在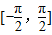 上的最大值与最小值分别为M与N,则有( )
上的最大值与最小值分别为M与N,则有( ) (
( 且
且 )
) 在
在 上的最大值与最小值的和为2,求
上的最大值与最小值的和为2,求 的值;
的值; 的图象,写函数
的图象,写函数 在
在 上的最大值与最小值之差为
上的最大值与最小值之差为 ,则
,则 。
。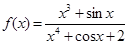 在
在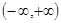 上的最大值与最小值分别为
上的最大值与最小值分别为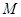 与
与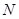 ,则有(
)
,则有(
)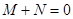 B.
B. 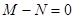 C.
C. D.
D.