题目内容
若函数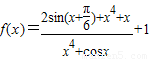 在
在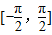 上的最大值与最小值分别为M与N,则有( )
上的最大值与最小值分别为M与N,则有( )A.M-N=2
B.M+N=2
C.M-N=4
D.M+N=4
【答案】分析:先对函数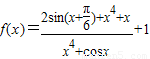 进行化简,变形后再其性质,由于其可以变为
进行化简,变形后再其性质,由于其可以变为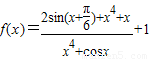 =
=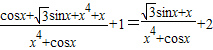 ,可令F(x)=f(x)-2=
,可令F(x)=f(x)-2= 是一个奇函数,利用此性质研究最大值与最小值的关系即可
是一个奇函数,利用此性质研究最大值与最小值的关系即可
解答:解:∵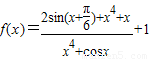 =
=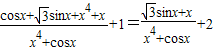 ,
,
令F(x)=f(x)-2=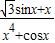 ,它是一个奇函数,
,它是一个奇函数,
∴F(x)的图象关于(0,0)对称
∴f(x)的图象关于(0,2)对称
由此知最大值与最小值和为4即M+N=4
故选D
点评:本题考查三角函数的最值,解题的关键是对函数的解析式进行化简研究出函数的性质,由函数的性质得出最值的关系,本题是一个探究型题,从研究其性质入手解决此类题是常用的方法,本题考查了推理判断的能力.
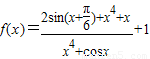 进行化简,变形后再其性质,由于其可以变为
进行化简,变形后再其性质,由于其可以变为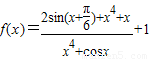 =
=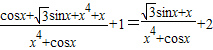 ,可令F(x)=f(x)-2=
,可令F(x)=f(x)-2= 是一个奇函数,利用此性质研究最大值与最小值的关系即可
是一个奇函数,利用此性质研究最大值与最小值的关系即可解答:解:∵
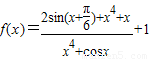 =
=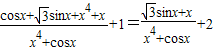 ,
,令F(x)=f(x)-2=
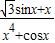 ,它是一个奇函数,
,它是一个奇函数,∴F(x)的图象关于(0,0)对称
∴f(x)的图象关于(0,2)对称
由此知最大值与最小值和为4即M+N=4
故选D
点评:本题考查三角函数的最值,解题的关键是对函数的解析式进行化简研究出函数的性质,由函数的性质得出最值的关系,本题是一个探究型题,从研究其性质入手解决此类题是常用的方法,本题考查了推理判断的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
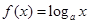
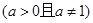 在
在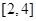 上的最大值与最小值之差为2,则
上的最大值与最小值之差为2,则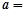 .
. (
( 且
且 )
) 在
在 上的最大值与最小值的和为2,求
上的最大值与最小值的和为2,求 的值;
的值; 的图象,写函数
的图象,写函数 在
在 上的最大值与最小值之差为
上的最大值与最小值之差为 ,则
,则 。
。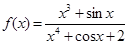 在
在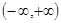 上的最大值与最小值分别为
上的最大值与最小值分别为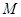 与
与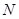 ,则有(
)
,则有(
)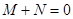 B.
B. 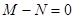 C.
C. D.
D.