题目内容
若双曲线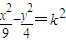 与圆x2+y2=1有公共点,则实数k的取值范围为 .
与圆x2+y2=1有公共点,则实数k的取值范围为 .
【答案】分析:假设双曲线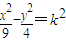 与圆x2+y2=1没有公共点,求出k的范围,然后再求补集即可;由双曲线
与圆x2+y2=1没有公共点,求出k的范围,然后再求补集即可;由双曲线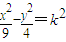 与圆x2+y2=1没有公共点知圆半径的长小于双曲线的实半轴的长,由此可以求出实数k的取值范围.
与圆x2+y2=1没有公共点知圆半径的长小于双曲线的实半轴的长,由此可以求出实数k的取值范围.
解答:解:s设双曲线 与圆x2+y2=1没有公共点,
与圆x2+y2=1没有公共点,
∴|3k|>1,∴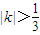 .
.
∴双曲线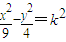 与圆x2+y2=1有公共点,则实数k的取值范围为实数k的取值范围为[-
与圆x2+y2=1有公共点,则实数k的取值范围为实数k的取值范围为[- ,0)∪(0,
,0)∪(0, ].
].
故答案为[- ,0)∪(0,
,0)∪(0, ].
].
点评:本题考查了双曲线的简单性质,熟练掌握圆和双曲线的图象和性质即可顺利求解.
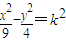 与圆x2+y2=1没有公共点,求出k的范围,然后再求补集即可;由双曲线
与圆x2+y2=1没有公共点,求出k的范围,然后再求补集即可;由双曲线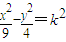 与圆x2+y2=1没有公共点知圆半径的长小于双曲线的实半轴的长,由此可以求出实数k的取值范围.
与圆x2+y2=1没有公共点知圆半径的长小于双曲线的实半轴的长,由此可以求出实数k的取值范围.解答:解:s设双曲线
 与圆x2+y2=1没有公共点,
与圆x2+y2=1没有公共点,∴|3k|>1,∴
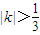 .
.∴双曲线
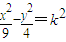 与圆x2+y2=1有公共点,则实数k的取值范围为实数k的取值范围为[-
与圆x2+y2=1有公共点,则实数k的取值范围为实数k的取值范围为[- ,0)∪(0,
,0)∪(0, ].
].故答案为[-
 ,0)∪(0,
,0)∪(0, ].
].点评:本题考查了双曲线的简单性质,熟练掌握圆和双曲线的图象和性质即可顺利求解.

练习册系列答案
相关题目
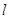 ,使得
,使得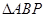 的面积最大时点P的坐标.
的面积最大时点P的坐标.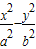 =1(a>0,b>0)的左、右焦点.
=1(a>0,b>0)的左、右焦点.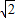 ,过F2的直线交双曲线于A,B两点,且以AB为直径的圆与y轴相切,求线段AB的长.
,过F2的直线交双曲线于A,B两点,且以AB为直径的圆与y轴相切,求线段AB的长.