题目内容
已知F1,F2为双曲线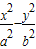 =1(a>0,b>0)的左、右焦点.
=1(a>0,b>0)的左、右焦点.(Ⅰ)若点P为双曲线与圆x2+y2=a2+b2的一个交点,且满足|PF1|=2|PF2|,求此双曲线的离心率;
(Ⅱ)设双曲线的渐近线方程为y=±x,F2到渐近线的距离是
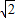 ,过F2的直线交双曲线于A,B两点,且以AB为直径的圆与y轴相切,求线段AB的长.
,过F2的直线交双曲线于A,B两点,且以AB为直径的圆与y轴相切,求线段AB的长.
【答案】分析:(Ⅰ)由双曲线的定义及|PF1|=2|PF2|求出|PF1|和|PF2|,给出的圆的半径为双曲线的半焦距,说明△F1PF2为直角三角形,利用勾股定理得关系式可求双曲线的离心率;
(Ⅱ)由双曲线的渐近线方程为y=±x,说明双曲线为等轴双曲线,再由F2到渐近线的距离是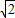 ,结合a2+b2=c2即可求出双曲线方程,利用双曲线的焦半径公式求出A(x1,y1),B(x2,y2)到F2的距离,根据以AB为直径的圆与y轴相切,得到
,结合a2+b2=c2即可求出双曲线方程,利用双曲线的焦半径公式求出A(x1,y1),B(x2,y2)到F2的距离,根据以AB为直径的圆与y轴相切,得到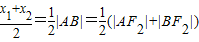 ,代入坐标后整理即可得到线段AB的长.
,代入坐标后整理即可得到线段AB的长.
解答:解:(Ⅰ)由题设得: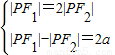 ,得|PF1|=4a,|PF2|=2a,
,得|PF1|=4a,|PF2|=2a,
因为点P为双曲线与圆x2+y2=a2+b2=c2的一个交点,∴PF1⊥PF2,
∴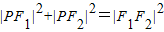 ,则16a2+4a2=4c2,即5a2=c2,故离心率
,则16a2+4a2=4c2,即5a2=c2,故离心率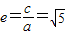 ;
;
(Ⅱ)∵双曲线的渐近线方程为y=±x,F2到渐近线的距离是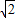 ,
,
∴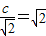 ,所以c=2,又
,所以c=2,又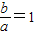 ,a2+b2=c2,得a=b=
,a2+b2=c2,得a=b=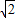 ,
,
所以双曲线方程为x2-y2=2,F2(2,0),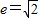 .
.
设A(x1,y1),B(x2,y2),由双曲线的焦半径公式得: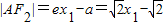 ,
,
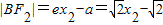 ,
,
∵以AB为直径的圆与y轴相切,∴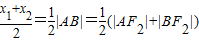 .
.
∴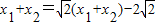 ,则
,则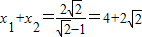 ,
,
所以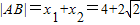 .
.
点评:本题考查双曲线的基本性质、双曲线方程的求法以及直线与双曲线的综合问题.直线与圆锥曲线联系在一起的综合题在高考中多以高档题、压轴题出现,主要涉及位置关系的判定,弦长问题、最值问题、对称问题、轨迹问题等.突出考查了数形结合、分类讨论、函数与方程、等价转化等数学思想方法.属难题.
(Ⅱ)由双曲线的渐近线方程为y=±x,说明双曲线为等轴双曲线,再由F2到渐近线的距离是
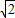 ,结合a2+b2=c2即可求出双曲线方程,利用双曲线的焦半径公式求出A(x1,y1),B(x2,y2)到F2的距离,根据以AB为直径的圆与y轴相切,得到
,结合a2+b2=c2即可求出双曲线方程,利用双曲线的焦半径公式求出A(x1,y1),B(x2,y2)到F2的距离,根据以AB为直径的圆与y轴相切,得到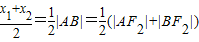 ,代入坐标后整理即可得到线段AB的长.
,代入坐标后整理即可得到线段AB的长.解答:解:(Ⅰ)由题设得:
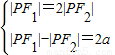 ,得|PF1|=4a,|PF2|=2a,
,得|PF1|=4a,|PF2|=2a,因为点P为双曲线与圆x2+y2=a2+b2=c2的一个交点,∴PF1⊥PF2,
∴
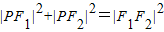 ,则16a2+4a2=4c2,即5a2=c2,故离心率
,则16a2+4a2=4c2,即5a2=c2,故离心率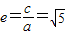 ;
;(Ⅱ)∵双曲线的渐近线方程为y=±x,F2到渐近线的距离是
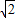 ,
,∴
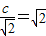 ,所以c=2,又
,所以c=2,又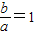 ,a2+b2=c2,得a=b=
,a2+b2=c2,得a=b=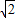 ,
,所以双曲线方程为x2-y2=2,F2(2,0),
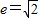 .
.设A(x1,y1),B(x2,y2),由双曲线的焦半径公式得:
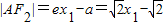 ,
,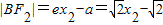 ,
,∵以AB为直径的圆与y轴相切,∴
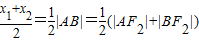 .
.∴
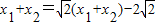 ,则
,则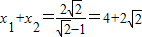 ,
,所以
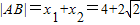 .
.点评:本题考查双曲线的基本性质、双曲线方程的求法以及直线与双曲线的综合问题.直线与圆锥曲线联系在一起的综合题在高考中多以高档题、压轴题出现,主要涉及位置关系的判定,弦长问题、最值问题、对称问题、轨迹问题等.突出考查了数形结合、分类讨论、函数与方程、等价转化等数学思想方法.属难题.

练习册系列答案
相关题目
已知F1,F2分别为双曲
-
=1(a>0,b>0)的左、右焦点,P为双曲线左支上任一点,若
的最小值为8a,则双曲线的离心率e的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
| |PF2|2 |
| |PF1| |
| A、(1,+∞) |
| B、(0,3] |
| C、(1,3] |
| D、(0,2] |
 的左、右焦点,P为双曲线左支上任一点,若
的左、右焦点,P为双曲线左支上任一点,若 的最小值为8a,则双曲线的离心率e的取值范围是( )
的最小值为8a,则双曲线的离心率e的取值范围是( ) 的左、右焦点,P为双曲线左支上任一点,若
的左、右焦点,P为双曲线左支上任一点,若 的最小值为8a,则双曲线的离心率e的取值范围是( )
的最小值为8a,则双曲线的离心率e的取值范围是( ) 的左、右焦点,P为双曲线左支上任一点,若
的左、右焦点,P为双曲线左支上任一点,若 的最小值为8a,则双曲线的离心率e的取值范围是( )
的最小值为8a,则双曲线的离心率e的取值范围是( )