题目内容
若α∥β，A∈α，C∈α，B∈β，D∈β，且AB+CD=28，AB、CD 在β内的射影长分别为9和5，则AB、CD的长分别为（ ）
分析：利用线面平行的性质、勾股定理即可得出．
解答：解：如图所示：分别经过点A，C作AE⊥β，CD⊥β，垂足分别为E，F，
∴BE=9，DF=5．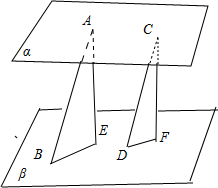
∵α∥β，∴AE=CF．
在Rt△ABE中，由勾股定理可得AE2=AB2-BE2．
在Rt△CDF中，由勾股定理可得CF2=CD2-DF2．
∴AB2-92=CD2-52，又AB+CD=28，联立解得
．
故选B．
∴BE=9，DF=5．
∵α∥β，∴AE=CF．
在Rt△ABE中，由勾股定理可得AE2=AB2-BE2．
在Rt△CDF中，由勾股定理可得CF2=CD2-DF2．
∴AB2-92=CD2-52，又AB+CD=28，联立解得
|
故选B．
点评：熟练掌握线面平行的性质、勾股定理、方程的思想方法是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目