题目内容
若|
|=2|
|≠0,
=
+
,且
⊥
,则向量
与
的夹角为
.
| b |
| a |
| c |
| a |
| b |
| c |
| a |
| a |
| b |
| 2π |
| 3 |
| 2π |
| 3 |
分析:利用向量垂直的充要条件及向量的数量积公式列出方程,求出夹角余弦,从而求出夹角.
解答:解:设
,
的夹角为θ
∵
⊥
∴
•
=0
∴(
+
)•
=0即
2+
•
=0
∴|
|2+|
||
||cosθ=0
∵|
=2|
|≠0
∴1+2cosθ=0
∴cosθ=-
∴θ=
故答案为:
| a |
| b |
∵
| c |
| a |
∴
| c |
| a |
∴(
| a |
| b |
| a |
| a |
| a |
| b |
∴|
| a |
| a |
| b |
∵|
| b |
| a |
∴1+2cosθ=0
∴cosθ=-
| 1 |
| 2 |
∴θ=
| 2π |
| 3 |
故答案为:
| 2π |
| 3 |
点评:本题考查两个向量的数量积的定义以及两个向量垂直的条件.考察基础知识,属于基础题目.

练习册系列答案
相关题目
已知向量
=(1,2),
=(x,4),若|
|=2|
|,则x的值为( )
| a |
| b |
| b |
| a |
| A、2 | B、4 | C、±2 | D、±4 |
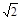 ,a=2,且三角形有解,则A的取值范围是( )
,a=2,且三角形有解,则A的取值范围是( )