题目内容
如图,斜率为 的直线过抛物线
的直线过抛物线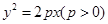 的焦点,与抛物线交于两点A、B, M为抛物线弧AB上的动点.
的焦点,与抛物线交于两点A、B, M为抛物线弧AB上的动点.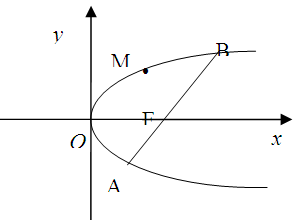
(Ⅰ).若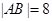 ,求抛物线的方程;
,求抛物线的方程;
(Ⅱ).求△ABM面积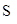 的最大值.
的最大值.
(I) 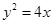 ;(II)
;(II)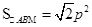 .
.
解析试题分析:(I) 写出直线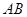 的方程
的方程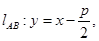 联立
联立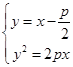 ,消去
,消去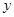 得
得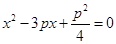 .根据弦长公式
.根据弦长公式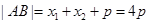 ,解得
,解得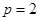 ,所以
,所以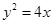 .(II)根据(I) 设
.(II)根据(I) 设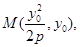
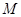 到
到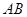 的距离:
的距离: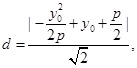 而M在直线AB上方,所以
而M在直线AB上方,所以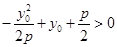 即
即 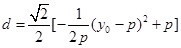 则
则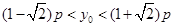 ,所以当
,所以当 时,
时, 取最大值
取最大值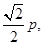 此时
此时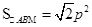 .
.
试题解析:(I) 根据条件得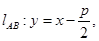 则
则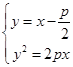 ,消去
,消去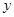 得
得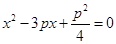 .
.
令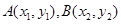 ,则
,则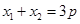 ,又抛物线定义得
,又抛物线定义得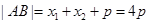
根据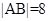 ,解得
,解得 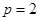 ,抛物线方程
,抛物线方程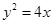 .
.
(II)由(I) 知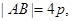
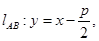 设
设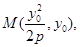 则
则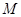 到
到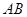 的距离:
的距离: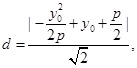
由M在直线AB上方,所以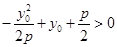 即
即 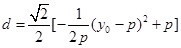 ,
,
由(I)知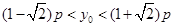
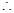 当
当 时,
时, 取最大值
取最大值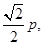 此时
此时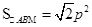 .
.
考点:1.直线与抛物线的联立;2.面积的求解.

练习册系列答案
相关题目
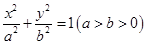 的左右两焦点分别为
的左右两焦点分别为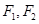 ,
,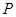 是椭圆上一点,且在
是椭圆上一点,且在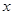 轴上方,
轴上方,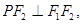
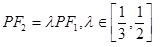 .
.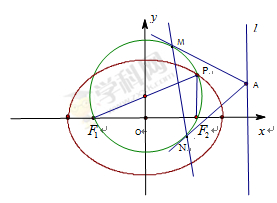
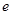 的取值范围;
的取值范围;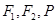 的圆
的圆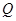 的截
的截 轴的线段长为6,求椭圆的方程;
轴的线段长为6,求椭圆的方程;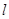 上任一点
上任一点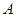 引圆
引圆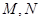 .试探究直线
.试探究直线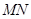 是否过定点?若过定点,请求出该定点;否则,请说明理由.
是否过定点?若过定点,请求出该定点;否则,请说明理由. 的直线过抛物线
的直线过抛物线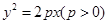 的焦点,与抛物线交于两点A、B, M为抛物线弧AB上的动点.
的焦点,与抛物线交于两点A、B, M为抛物线弧AB上的动点.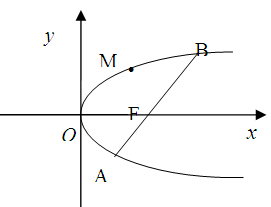
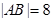 ,求抛物线的方程;
,求抛物线的方程;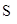 的最大值.
的最大值. ,动圆P过定点F与定直线相切,记动圆圆心P的轨迹为曲线C
,动圆P过定点F与定直线相切,记动圆圆心P的轨迹为曲线C 的顶点为原点,其焦点
的顶点为原点,其焦点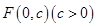 到直线
到直线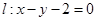 的距离为
的距离为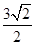 .设
.设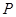 为直线
为直线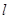 上的点,过点
上的点,过点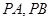 ,其中
,其中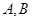 为切点.
为切点.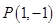 为直线
为直线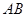 的方程;
的方程; 在直线
在直线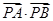 的最小值.
的最小值.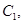 抛物线
抛物线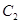 的焦点均在
的焦点均在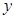 轴上,
轴上,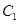 的中心和
的中心和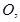 从每条曲线上取两个点,将其坐标记录于下表中:
从每条曲线上取两个点,将其坐标记录于下表中:

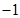
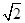
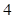
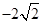
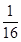
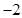
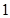
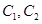 的方程的点的坐标;
的方程的点的坐标;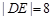 ,动点C的运动轨迹为曲线G,且当动点C运动时,
,动点C的运动轨迹为曲线G,且当动点C运动时,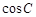 有最小值
有最小值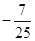 .
.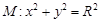 (其中
(其中 )于A、B两点,求|AB|的取值范围.
)于A、B两点,求|AB|的取值范围.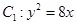 与双曲线
与双曲线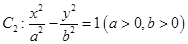 有公共焦点
有公共焦点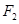 ,点
,点 是曲线
是曲线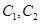 在第一象限的交点,且
在第一象限的交点,且 .
. 的方程;
的方程;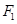 为圆心的圆
为圆心的圆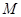 与直线
与直线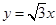 相切,圆
相切,圆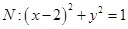 .过点
.过点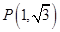 作互相垂直且分别与圆
作互相垂直且分别与圆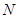 相交的直线
相交的直线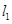 和
和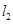 ,设
,设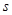 ,
, ,问:
,问: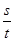 是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
是否为定值?如果是,请求出这个定值;如果不是,请说明理由.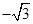 ,0),B(
,0),B(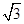 ,0),直线AM、BM相交于点M,且它们的斜率之积为
,0),直线AM、BM相交于点M,且它们的斜率之积为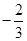 .
.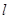 过点F(1,0)且绕F旋转,
过点F(1,0)且绕F旋转,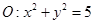 相交于P、Q两点,
相交于P、Q两点,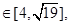 求△
求△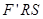 的面积的最大值和最小值(F′为轨迹C的左焦点).
的面积的最大值和最小值(F′为轨迹C的左焦点).