题目内容
已知椭圆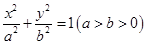 的左右两焦点分别为
的左右两焦点分别为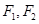 ,
,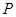 是椭圆上一点,且在
是椭圆上一点,且在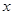 轴上方,
轴上方,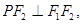
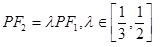 .
.
(1)求椭圆的离心率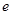 的取值范围;
的取值范围;
(2)当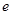 取最大值时,过
取最大值时,过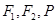 的圆
的圆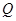 的截
的截 轴的线段长为6,求椭圆的方程;
轴的线段长为6,求椭圆的方程;
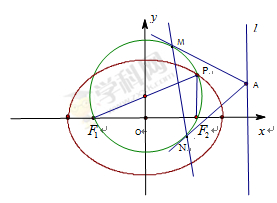
(3)在(2)的条件下,过椭圆右准线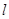 上任一点
上任一点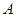 引圆
引圆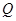 的两条切线,切点分别为
的两条切线,切点分别为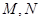 .试探究直线
.试探究直线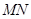 是否过定点?若过定点,请求出该定点;否则,请说明理由.
是否过定点?若过定点,请求出该定点;否则,请说明理由.
(1)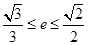 ;(2)
;(2)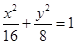 ;(3)
;(3)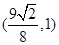 .
.
解析试题分析:(1)由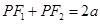 ,
,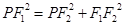 ,
,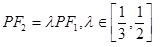 .即可求得
.即可求得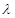 的取值范围.
的取值范围.
(2)由(1)可得 .以及
.以及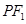 是圆的直径可得
是圆的直径可得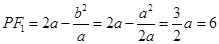 .即可求出椭圆的方程.
.即可求出椭圆的方程.
(3)由(2)可得圆Q的方程.切点M,N所在的圆的方程上任一点坐标为P(x,y).由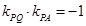 .即得
.即得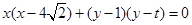 .则M,N所在的直线方程为.两圆方程对减即可得到.根据过定点的知识即可求出定点.本题涉及的知识点较多,渗透方程的思想,加强对几何图形的关系理解.
.则M,N所在的直线方程为.两圆方程对减即可得到.根据过定点的知识即可求出定点.本题涉及的知识点较多,渗透方程的思想,加强对几何图形的关系理解.
试题解析: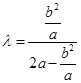 , ∴
, ∴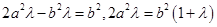 ,
,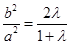 .
.
(1) ,∴
,∴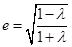 ,在
,在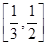 上单调递减.
上单调递减.
∴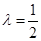 时,
时,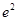 最小
最小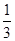 ,
,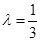 时,
时,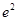 最大
最大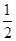 ,∴
,∴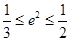 ,∴
,∴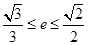 .
.
(2)当 时,
时,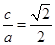 ,∴
,∴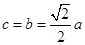 ,∴
,∴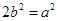 .
.
∵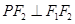 ,∴
,∴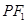 是圆的直径,圆心是
是圆的直径,圆心是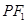 的中点,∴在y轴上截得的弦长就是直径,∴
的中点,∴在y轴上截得的弦长就是直径,∴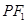 =6.又
=6.又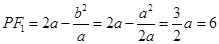 ,∴
,∴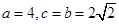 .∴椭圆方程是
.∴椭圆方程是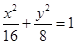 10分
10分
(3)由(2)得到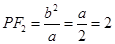 ,于是圆心
,于是圆心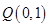 ,半径为3,圆
,半径为3,圆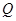 的方程是
的方程是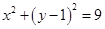 .椭圆的右准线方程为
.椭圆的右准线方程为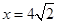 ,,∵直线AM,AN是圆Q的两条切线,∴切点M,N在以AQ为直径的圆上.设A点坐标为
,,∵直线AM,AN是圆Q的两条切线,∴切点M,N在以AQ为直径的圆上.设A点坐标为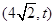 ,∴该圆方程为
,∴该圆方程为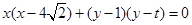 .∴直线MN是两圆的公共弦,两圆方程相减得:
.∴直线MN是两圆的公共弦,两圆方程相减得: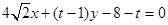 ,这就是直线MN的方程.该直线化为:
,这就是直线MN的方程.该直线化为: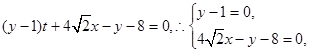
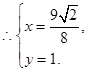
∴直线MN必过定点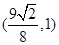 . 16分
. 16分
考点:1.椭圆的离心率.2.椭圆的标准方程.3.两圆的公共线的方程.4.过定点问题.

练习册系列答案
相关题目
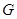 :
: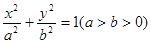 的离心率为
的离心率为 ,过椭圆
,过椭圆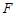 的直线
的直线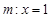 与椭圆
与椭圆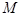 (点
(点 为椭圆
为椭圆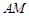 的直线
的直线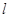 与椭圆相交于
与椭圆相交于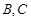 两点.判断直线
两点.判断直线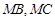 是否关于直线
是否关于直线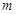 对称,并说明理由.
对称,并说明理由.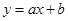 与双曲线
与双曲线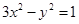 交于A、B,且以AB为直径的圆过原点,求点
交于A、B,且以AB为直径的圆过原点,求点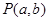 的轨迹方程.
的轨迹方程.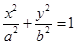
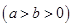 的左、右焦点分别是
的左、右焦点分别是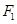 、
、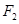 ,
, 是椭圆右准线上的一点,线段
是椭圆右准线上的一点,线段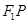 的垂直平分线过点
的垂直平分线过点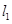 :
: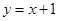 按向量
按向量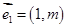 平移后的直线是
平移后的直线是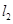 ,直线
,直线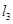 :
: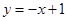 按向量
按向量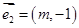 平移后的直线是
平移后的直线是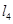 (其中
(其中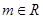 )。
)。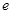 的取值范围。
的取值范围。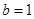 时,求椭圆的方程。
时,求椭圆的方程。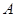 、
、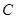 两点,
两点,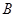 、
、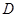 两点。求四边形ABCD面积
两点。求四边形ABCD面积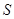 的取值范围。
的取值范围。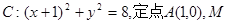 为圆上一动点,点
为圆上一动点,点 是线段
是线段 的垂直平分线与直线
的垂直平分线与直线 的交点.
的交点.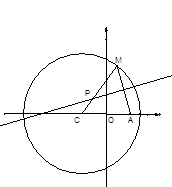
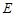 的方程;
的方程;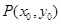 是曲线
是曲线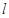 的方程;(不要求证明)
的方程;(不要求证明)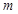 过切点
过切点 关于直线
关于直线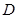 ,证明:直线
,证明:直线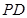 恒过一定点,并求定点的坐标.
恒过一定点,并求定点的坐标.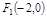 、
、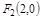 ,动点N满足
,动点N满足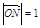 (O为坐标原点),
(O为坐标原点),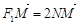 ,
,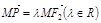 ,
, ,求点P的轨迹方程.
,求点P的轨迹方程.
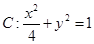 的上、下顶点分别为
的上、下顶点分别为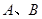 ,点
,点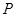 在椭圆上,且异于点
在椭圆上,且异于点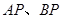 与直线
与直线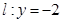 分别交于点
分别交于点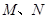 ,
,
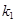 、
、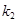 ,求证:
,求证: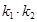 为定值;
为定值;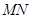 为直径的圆是否经过定点?请证明你的结论.
为直径的圆是否经过定点?请证明你的结论.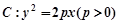 上有一点
上有一点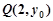 ,到焦点
,到焦点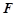 的距离为
的距离为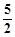 .
.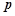 及
及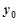 的值.
的值. 与抛物线交于两点
与抛物线交于两点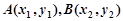 ,且
,且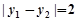 ,过弦
,过弦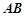 的中点
的中点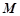 作垂直于
作垂直于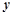 轴的直线与抛物线交于点
轴的直线与抛物线交于点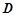 ,连接
,连接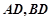 .试判断
.试判断 的面积是否为定值?若是,求出定值;否则,请说明理由.
的面积是否为定值?若是,求出定值;否则,请说明理由.
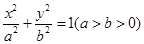 的左焦点为
的左焦点为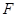 ,离心率为
,离心率为 ,过点
,过点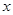 轴垂直的直线被椭圆截得的线段长为
轴垂直的直线被椭圆截得的线段长为
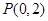 的直线
的直线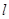 与椭圆交于不同的两点
与椭圆交于不同的两点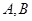 ,当
,当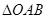 面积最大时,求
面积最大时,求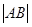
 的直线过抛物线
的直线过抛物线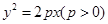 的焦点,与抛物线交于两点A、B, M为抛物线弧AB上的动点.
的焦点,与抛物线交于两点A、B, M为抛物线弧AB上的动点.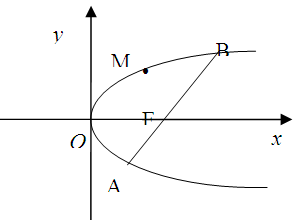
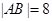 ,求抛物线的方程;
,求抛物线的方程;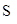 的最大值.
的最大值.