题目内容
已知
则
= ．
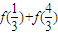【答案】分析：因为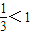
，所以可以直接求出：
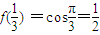，对于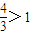
，用表达式的定义得
，
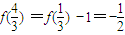从而得出要求的答案．
解答：解：∵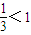
∴
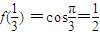
而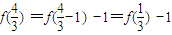
=
∴
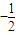
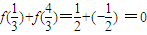
故答案为：0
点评：本题考查了分段函数的解析式的理解，并用其解函数值，属于基础题．注意解题时的处理：分段函数分段讨论，最后综合求各部分的情况得到答案．
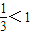，所以可以直接求出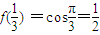：，对于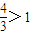，用表达式的定义得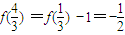，从而得出要求的答案．
解答：解：∵
∴
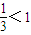
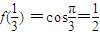
而
=
∴
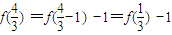
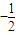
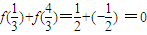
故答案为：0
点评：本题考查了分段函数的解析式的理解，并用其解函数值，属于基础题．注意解题时的处理：分段函数分段讨论，最后综合求各部分的情况得到答案．
练习册系列答案
名师指导期末冲刺卷系列答案
开心蛙口算题卡系列答案
相关题目
已知则∫-aacosxdx=
（a＞0），则∫0acosxdx=（ ）
| 1 |
| 2 |
| A、2 | ||
| B、1 | ||
C、
| ||
D、
|
则
的最小值是_____________.
,则两圆x2+y2=r2与(x-1)2+(y+1)2=2的位置关系是( ) 
则
，
，
；