Question

设函数f（x）=x²+|x-a|（x∈R，a∈R）．
（1）讨论f（x）的奇偶性；
（2）当a=1时，求f（x）的单调区间；
（3）若f（x）＜10对x∈（-1，3）恒成立，求实数a的取值范围．

Answer 1

分析：（1）当a=0时，f（x）为偶函数；当a≠0时，f（x）为非奇非偶函数；
（2）a=1时，f（x）=x²+|x-1|=

x2+x-1，x≥1 x2-x+1，x＜1

，再进行配方，利用函数的图象，确定函数的单调区间；
（3）f（x）=x²+|x-a|＜10对x∈（-1，3）恒成立，等价于x²-10＜x-a＜10-x²，分离参数可得

a＜-(x- 1 2 )2+10 1 4 a＞(x+ 1 2 )2-10 1 4

对x∈（-1，3）恒成立，从而可求实数a的取值范围．

解答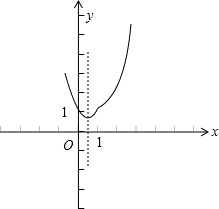：解：（1）当a=0时，f（x）为偶函数；当a≠0时，f（x）为非奇非偶函数
（2）a=1时，f（x）=x²+|x-1|=

x2+x-1，x≥1 x2-x+1，x＜1

=

(x+ 1 2 )2- 5 4 ，x≥1 (x- 1 2 )2+ 3 4 ，x＜1

∴函数的单调减区间为（-∞，

1

2

），函数的单调增区间为（

1

2

，+∞）
（3）f（x）=x²+|x-a|＜10对x∈（-1，3）恒成立，等价于x²-10＜x-a＜10-x²，
等价于

a＜-(x- 1 2 )2+10 1 4 a＞(x+ 1 2 )2-10 1 4

对x∈（-1，3）恒成立
∴2≤a≤4

点评：本题考查带绝对值的函数，考查分类讨论、数形结合的数学思想，考查恒成立问题，综合性较强．