题目内容
2.设左右焦点分别为F1、F2的椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,P为椭圆C上任意一点,且$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$的最小值为2.(1)求椭圆C的方程;
(2)过坐标原点O作两条互相垂直的射线,与椭圆C分别交于A、B两点,证明:直线AB与圆x2+y2=$\frac{12}{7}$相切.
分析 (1)设P(x,y),则x2+y2=$\frac{{c}^{2}}{{a}^{2}}{x}^{2}$+b2≥b2.而$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=x2-c2+y2≥2.可得b2=c2+2,又$\frac{c}{a}$=$\frac{1}{2}$,a2=b2+c2,联立解出即可.
(2)设A(x1,y1),B(x2,y2),当直线AB的斜率存在时,设直线AB的方程为:y=kx+m.与椭圆方程联立化为:(3+4k2)x2+8kmx+4m2-12=0,△>0,由于OA⊥OB,可得x1x2+y1y2=0,利用根与系数的关系可得7m2=12(k2+1).即可得出圆的O到直线AB的距离d=$\frac{|m|}{\sqrt{1+{k}^{2}}}$=R.即可证明结论.当直线AB的斜率不存在时,容易证明直线AB与圆x2+y2=$\frac{12}{7}$相切.
解答 (1)解:设P(x,y),则x2+y2=${x}^{2}+{b}^{2}(1-\frac{{x}^{2}}{{a}^{2}})$=$\frac{{c}^{2}}{{a}^{2}}{x}^{2}$+b2≥b2.
∵$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=(-c-x,-y)•(c-x,-y)=x2-c2+y2≥2.
∴b2=c2+2,
又$\frac{c}{a}$=$\frac{1}{2}$,a2=b2+c2,
解得c2=1,b2=3,a=2.
∴椭圆C的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$.
(2)证明:设A(x1,y1),B(x2,y2),
当直线AB的斜率存在时,设直线AB的方程为:y=kx+m.
联立$\left\{\begin{array}{l}{y=kx+m}\\{3{x}^{2}+4{y}^{2}=12}\end{array}\right.$,
化为:(3+4k2)x2+8kmx+4m2-12=0,
△>0,
∴x1+x2=$\frac{-8km}{3+4{k}^{2}}$,x1x2=$\frac{4{m}^{2}-12}{3+4{k}^{2}}$.
∵OA⊥OB,
∴x1x2+y1y2=0,
∴x1x2+(kx1+m)(kx2+m)=(1+k2)x1x2+mk(x1+x2)+m2
=$\frac{(1+{k}^{2})(4{m}^{2}-12)}{3+4{k}^{2}}$-$\frac{8{k}^{2}{m}^{2}}{3+4{k}^{2}}$+m2=0,
化为:7m2=12(k2+1).
∴圆的O到直线AB的距离d=$\frac{|m|}{\sqrt{1+{k}^{2}}}$=$\sqrt{\frac{7}{12}}$=R.
∴直线AB与圆x2+y2=$\frac{12}{7}$相切.
当直线AB的斜率不存在时,容易证明直线AB与圆x2+y2=$\frac{12}{7}$相切.
综上可得:直线AB与圆x2+y2=$\frac{12}{7}$相切.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题、直线与圆相切问题、一元二次方程的根与系数的关系、点到直线的距离公式、相互垂直的直线斜率之间的关系、数量积运算性质,考查了推理能力与计算能力,属于难题.

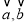 ,满足
,满足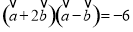 ,且
,且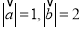 ,则
,则 与
与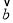 的夹角为( )
的夹角为( )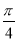 B.
B.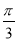 C.
C.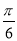 D.
D.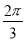
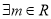 ,使
,使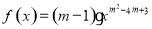 是幂函数,且在
是幂函数,且在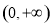 上递减
上递减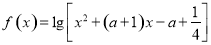 的值域为
的值域为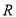 ,则
,则
 的方程
的方程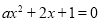 至少有一个负根的弃要条件是
至少有一个负根的弃要条件是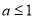
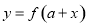 与函数
与函数 的图像关于直线
的图像关于直线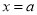 对称
对称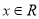 ,则“
,则“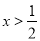 ”是“
”是“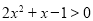 ”的( )
”的( )